题目内容
数字3可以有四种方式表达为1个或几个正整数的有序和3,1+2,2+1,l+l+1,那么对于一般的正整数n,如此表达方式的个数为________.
2n-1
分析:一个有序的和a1+a2+…+aK=n,ai≥1可以用排成一行的个1被个斜杠“/”分割开的形式来表达,即111…1/11…1/11…1/…/11…1其中第1部分含a个1,第2部分含a2个1,第3部分含a3个1,…,最后的第k部分含ak个1.为了得到所有这样的表达形式(对所有的1≤k≤n),可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放,这样就可产生2n-1种不同的表达形式.
解答:∵正整数n用排成一行的个1被个斜杠“/”分割开的形式来表达,111…1/11…1/11…1/…/11…1,
其中第1部分含a个1,第2部分含a2个1,第3部分含a3个1,…,最后的第k部分含ak个1.
对所有的1≤k≤n,可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放,
∴可产生2n-1种不同的表达形式.
故答案为:2n-1.
点评:本题考查了正整数的有序和的规律,解题的关键是得出所有的1≤k≤n,可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放.
分析:一个有序的和a1+a2+…+aK=n,ai≥1可以用排成一行的个1被个斜杠“/”分割开的形式来表达,即111…1/11…1/11…1/…/11…1其中第1部分含a个1,第2部分含a2个1,第3部分含a3个1,…,最后的第k部分含ak个1.为了得到所有这样的表达形式(对所有的1≤k≤n),可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放,这样就可产生2n-1种不同的表达形式.
解答:∵正整数n用排成一行的个1被个斜杠“/”分割开的形式来表达,111…1/11…1/11…1/…/11…1,
其中第1部分含a个1,第2部分含a2个1,第3部分含a3个1,…,最后的第k部分含ak个1.
对所有的1≤k≤n,可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放,
∴可产生2n-1种不同的表达形式.
故答案为:2n-1.
点评:本题考查了正整数的有序和的规律,解题的关键是得出所有的1≤k≤n,可以将n个l排成一行,在每相邻两个1之间产生的n-1个空位中,要么放上一个斜杠,要么不放.

练习册系列答案
相关题目
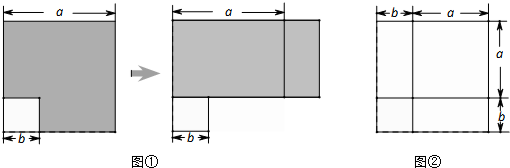
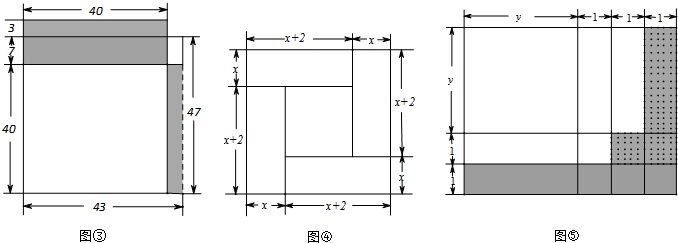




 ,宽为
,宽为 的矩形,构造图④
的矩形,构造图④
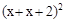 或四个长
或四个长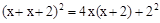




 的解
的解 与
与 的大小关系(其中
的大小关系(其中 )?
)? ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割

 ,
, ,即
,即 ,
,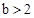 时,表示
时,表示 与
与 的大小关系
的大小关系 ,
,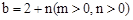 ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)