题目内容
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第一象限内作等边△AOB,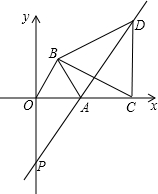 点C在x的正半轴上,且OC>1,连接BC,以线段BC为边在第一象限内作等边△CBD.
点C在x的正半轴上,且OC>1,连接BC,以线段BC为边在第一象限内作等边△CBD.(1)求证:△OBC≌△ABD;
(2)当点C沿x轴向右移动时,直线DA交y轴于点P,求点P坐标.
分析:(1)由等边△AOB,等边△CBD得OB=AB,BC=BD,∠OBA=∠CBD=60°,所以,∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,从而△OBC≌△ABD.
(2)由(1)得∠BAD=∠BOC=60°,可推出∠OAP=60°,在直角三角形OAP中,OA=1,则求出OP,从而求出点P坐标.
(2)由(1)得∠BAD=∠BOC=60°,可推出∠OAP=60°,在直角三角形OAP中,OA=1,则求出OP,从而求出点P坐标.
解答:(1)证明:已知等边△AOB,等边△CBD,∴∠OBA=∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
∴OB=AB,BC=BD,
∴△OBC≌△ABD.
(2)解:由(1)可知∠BAD=∠BOC=60°,
∵∠OAP+∠OAB+∠BAD=180°,∴∠OAP=60°.
在△OAP中,∠AOP=90°,tan∠OAP=
,
∴OP=OA•tan60°=
.(7分)
∴当点C沿x轴向右移动时,求点P的坐标为(0,-
).
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
∴OB=AB,BC=BD,
∴△OBC≌△ABD.
(2)解:由(1)可知∠BAD=∠BOC=60°,
∵∠OAP+∠OAB+∠BAD=180°,∴∠OAP=60°.
在△OAP中,∠AOP=90°,tan∠OAP=
| OP |
| OA |
∴OP=OA•tan60°=
| 3 |
∴当点C沿x轴向右移动时,求点P的坐标为(0,-
| 3 |
点评:此题考查的知识点是解直角三角形、坐标与图形性质,关键是两等边三角形证明三角形全等,及推出∠OAP=60°通过解直角三角形求P的坐标.

练习册系列答案
相关题目
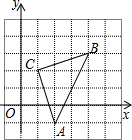 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: