题目内容
用换元法解方程
+
=6，若设y=
，则原方程可化为（ ）
| x2-2 |
| x+1 |
| 8(x+1) |
| x2-2 |
| x2-2 |
| x+1 |
| A、y2+6y+8=0 |
| B、y2-6y+8=0 |
| C、y2+8y-6=0 |
| D、y2+8y+6=0 |
考点：换元法解分式方程
专题：
分析：根据y=
，进而代入原方程求出即可．
| x2-2 |
| x+1 |
解答：解：∵设y=
，则原方程可化为：y+
=6，
∴y2-6y+8=0．
故选；B．
| x2-2 |
| x+1 |
| 8 |
| y |
∴y2-6y+8=0．
故选；B．
点评：此题主要考查了换元法解分式方程，将原式中式式子用y代替得出是解题关键．
练习册系列答案
相关题目
如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长．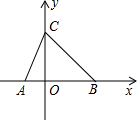
如图，点A为x轴负半轴上一点，点B为x轴正半轴上一点，OA、OB（OA＜0B）的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根，C（0，3），且△ABC的面积为6，求∠ABC的度数．下列说法正确的是（ ）
| A、底角相等的两个等腰三角形全等 |
| B、等腰三角形的中线、高、角平分线互相重合 |
| C、“同位角相等”是一个命题 |
| D、在同一个三角形中，有两个底角相等的三角形是等腰三角形 |