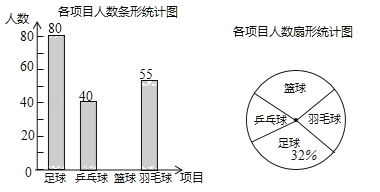
��Ŀ����
����Ŀ���ۺ���
��1����ͼ1����CO��AB������ΪO��OE��OF�ֱ�ƽ�֡�AOC���BOC�����EOF�Ķ�����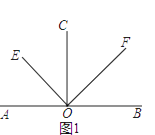
��2����ͼ2������AOC=��BOD=80�㣬OE��OF�ֱ�ƽ�֡�AOD���BOC�����EOF�Ķ�����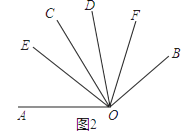
��3������AOC=��BOD=��������BOD�Ƶ�O��ת��ʹ������OC������OD�ļн�Ϊ�£�OE��OF�ֱ�ƽ�֡�AOD���BOC������+�¡�180�㣬�����£����EOC= �� ���ú�����µĴ���ʽ��ʾ��
���𰸡�
��1���⣺��CO��AB��
���AOC=��BOC=90�㣬
��OEƽ�֡�AOC��
���EOC= ![]() ��AOC=
��AOC= ![]() ��90��=45�㣬
��90��=45�㣬
��OFƽ�֡�BOC��
���COF= ![]() ��BOC=
��BOC= ![]() ��90��=45�㣬
��90��=45�㣬
��EOF=��EOC+��COF=45��+45��=90�㣻
��2���⣺��OEƽ�֡�AOD��
���EOD= ![]() ��AOD=
��AOD= ![]() ����80+�£�=40+
����80+�£�=40+ ![]() �£�
�£�
��OFƽ�֡�BOC��
���COF= ![]() ��BOC=
��BOC= ![]() ����80+�£�=40+
����80+�£�=40+ ![]() �£�
�£�
��COE=��EOD����COD=40+ ![]() �©���=40��
�©���=40�� ![]() �£�
�£�
��EOF=��COE+��COF=40�� ![]() ��+40+
��+40+ ![]() ��=80�㣻
��=80�㣻
��3��![]()
����������3����ͼ2���ߡ�AOC=��BOD=������COD=�£�
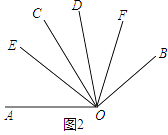
���AOD=��+�£�
��OEƽ�֡�AOD��
���DOE= ![]() ����+�£���
����+�£���
���COE=��DOE����COD= ![]() ��
��
��ͼ3���ߡ�AOC=��BOD=������COD=�£�
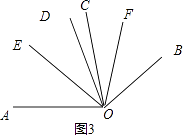
���AOD=��+�£�
��OEƽ�֡�AOD��
���DOE= ![]() �������£���
�������£���
���COE=��DOE+��COD= ![]() ��
��
���������� ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫�������ýǵ�ƽ���ߺͽǵ��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��һ���ǵĶ���������һ�����ߣ�������Ƿֳ�������ȵĽǣ��������߽�������ǵ�ƽ���ߣ���֮����Խ��мӼ����㣻һ���ǿ����������ǵĺͻ������ʾ��