Question

如图，AB为⊙·的直径，弦CD⊥AB，垂足为点M，AE切⊙·于点A，交BC的延长线于点E，连接AC．

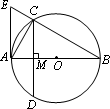
(1)若∠B＝30°，AB＝2，求CD的长；

(2)求证：AE²＝EB·EC．

Answer 1

答案：
解析：

解：(1)解法一： 　　∵AB为⊙·的直径， 　　∴∠ACB＝90°　　1分 　　∵在Rt△ABC中，∠B＝30°，AB＝2， 　　∴BC＝AB·c·s30°＝2×．2分 　　∵弦CD⊥直径AB，∠B＝30°， 　　∴ CM＝BC＝．　　4分 　　CD＝2CM＝．　　5分 　　解法二： 　　∵AB为⊙·的直径，∠B＝30°， 　　∴AC＝AB＝1，BC＝AB·c·s30°＝　　2分 　　∵弦CD⊥直径AB于点M， 　　∴CD＝2CM，AB×CM＝AC×BC　　4分 　　∴CD＝2CM＝2× 　　＝2×＝　　5分 　　(其它解法请酌情给分) 　　(2)证明：∵AE切⊙·于点A，AB为⊙·的直径， 　　∴∠BAE＝90°，∠ACE＝∠ACB＝90°，　　6分 　　∴∠ACE＝∠BAE＝90°．7分 　　又∵∠E＝∠E， 　　∴Rt△ECA∽Rt△EAB．8分 　　∴　　9分 　　∴AE2＝EB·EC　　10分