Question

【题目】在平面直角坐标系中，点O为坐标原点，纵坐标为a的点A在y轴上，横坐标为b的点B在x轴上，实数a，b满足|a+b﹣8|+（3a﹣2b+1）2＝0

（1）求a，b的值；

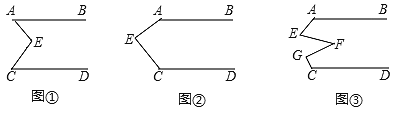
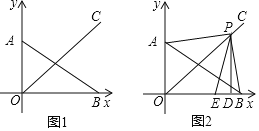
（2）如图1，第一象限的点P在∠AOB的平分线OC上，过点P作x轴的垂线，点D为垂足，设线段PD的长为d，△PAB的面积为S（S≠0）用含d的式子表示S，并直接写出相应的d的范围

（3）在（2）的条件下，如图2，当PA⊥PB时，点E在x轴上，连接PE，∠APE＝2∠ABO，求PE的长．

Answer 1

【答案】（1）a=3，b=5；（2）S=；（3）PE=.

【解析】

（1）由绝对值和平方的非负性可知，a+b-8=0，3a-2b+1=0，联立成方程组即求得a、b的值．

（2）过点P作PH⊥y轴于点H，由角平分线性质可得PH=PD=d，即d为△OAP与△OBP分别以OA、OB为底时的高．求直线AB、OC解析式，联立方程组求得交点R的坐标，即得到点P在线段OR上和射线RC上的范围．当点P在线段OR上时，△PAB面积等于△OAB面积减去△OAP、OBP面积的和；当点P在射线RC上时，△PAB面积等于△OAP、△OBP面积的和减去△OAB面积，代入计算即得到S关于d的函数关系式．

（3）先证∠PBO=∠HAP，再证△PAH≌△PBD，进而得△APB是等腰直角三角形，所以∠PAB=∠POB=45°，由三角形内角和180°转换得∠APO=∠ABO．再由∠APE=2∠ABO证得∠APO=∠EPO，进而得△AOP≌△EOP，PA=PE=PB，OA=OE=3，DE=BD=1，求得PD=OD=4，最后用勾股定理求得PE的长．

解：（1），

由，，

得，解得：.

（2）设交于点，

过点作轴于，则，

当点在线段上（不包括端点，）时，相应的的范围为.

当点在射线上（不包括端点）时，相应的的范围为.

∴S=；

（3）∵，

∴，

∴

且，

∴，

∵.

∵平分,，，

∴.

∴，

∴，且，

∴是等腰直角三角形，

∴且，，

∴，

∵，

∴，且，，

∴，

∴，，

∴，

∴，

∴，

∴，

∴.