题目内容
如图10,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线.
(2)当OA=3,AE=4时,求BC的长度.

解:(1)证明:连结OD.
∵OD=OA,EA=ED,
∴∠3=∠4, ∠1=∠2
∴∠1+∠3=∠2+∠4 , 即∠ODE=∠OAE
∵AB⊥AC, ∠OAE=90°
∴∠ODE=90°∴DE是⊙O的切线.
(2)∵OA=3, AE=4 ∴OE=5
又∵AB是直径, ∴AD⊥BC
∴∠1+∠5=9 0°,∠2+∠6=90°
0°,∠2+∠6=90°
又∵∠1=∠2 ∴∠5=∠6 ,∴DE=EC,
∴E是AC的中点.
∴OE∥BC且 OE= BC
BC
∴BC=10
 |

练习册系列答案
相关题目
若点A关于x轴的对称点为(﹣2,3),则点A关于y轴的对称点为( )
|
| A. | (﹣2,﹣3) | B. | (2,﹣3) | C. | (﹣2,3) | D. | (2,3) |

 的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,
的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内, 随
随 的增大而减小;③它的图象在二、四象限内.其中正确的是________________.
的增大而减小;③它的图象在二、四象限内.其中正确的是________________.
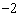 C.6 D.
C.6 D.
 的倒数是【 】
的倒数是【 】 B.
B. C.
C. D.
D. 中,
中, ,
, ,
, ,
,  ,
, 交
交 于
于 ,则△
,则△ 的周长为 .
的周长为 .