Question

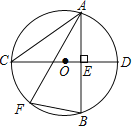
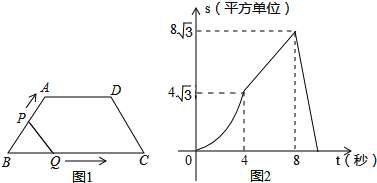
【题目】如图1，在等腰梯形ABCD中，∠B=60°，P、Q同时从B出发，以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒)，△BPQ的面积为S(平方单位)，S与t的函数图象如图2，则下列结论错误的个数有( )

①当t=4秒时，S=；②AD=4；③当4≤t≤8时，S=；④当t=9秒时，BP平分梯形ABCD的面积.

A.1B.2C.3D.4

Answer 1

【答案】A

【解析】

先判断△BPQ为等边三角形，然后表示出△BPQ的面积可判断①；由图像可判断②；用待定系数法求出EF的解析式可判断③；设梯形高为h，分别表示出梯形的面积和△BCP的面积可判断④.

解：如图2所示，动点运动过程分为三个阶段：

（1）OE段，函数图象为抛物线，运动图形如图1-1所示．

此时点P在线段AB上、点Q在线段BC上运动．

∵BP=BQ=t，∠B=60°，

∴△BPQ为等边三角形，

作PH⊥BQ于H，

∵sinB=,

∴PH= t，

∴S=．

由函数图象可知，当t=4秒时，S=4，故选项①正确．

（2）EF段，函数图象为直线，运动图形如图1-2所示．

此时点P在线段AD上、点Q在线段BC上运动．

由函数图象可知，此阶段运动时间为4s，

∴AD=1×4=4，故选项②正确．

设直线EF的解析式为：S=kt+b，将E（4，4）、F（8，8）代入得：

，

解得，

∴S=t，故选项③错误．

（3）FG段，函数图象为直线，运动图形如图1-3所示．

此时点P、Q均在线段CD上运动．

设梯形高为h，则S梯形ABCD=（AD+BC）h=（4+8）h=6h；

当t=9s时，DP=1，则CP=3，

∴CP：CD=3:4，

作DE⊥BC于E，PF⊥BC于F，则PF∥DE，

∴PF：DE=CP：CD=3:4，

∴PF=，

∴S△BCP=S△BCD=3h，

∴S△BCP=S梯形ABCD，即BP平分梯形ABCD的面积，故选项④正确．

故选：A．