Question

【题目】如图，在矩形中，，，是上的一个动点．

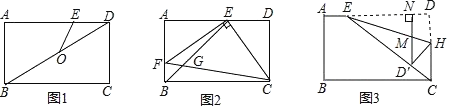
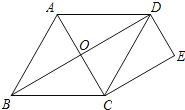
(1)如图1，连接，是对角线的中点，连接．当时，求的长；

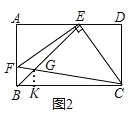
(2)如图2，连接，过点作交于点，连接，与交于点．当平分时，求的长；

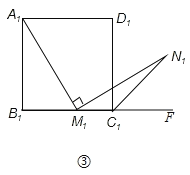
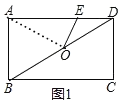
(3)如图3，连接，点在上，将矩形沿直线折叠，折叠后点落在上的点处，过点作于点，与交于点，且．

①求的值；

②连接，与是否相似？请说明理由．

Answer 1

【答案】(1)；(2)；(3)①；②相似，理由见解析.

【解析】

（1）先求出BD，进而求出OD=OB=OA，再判断出△ODE∽△ADO，即可得出结论；
（2）先判断出△AEF≌△DCE，进而求出BF=1，再判断出△CHG∽△CBF，进而求出，最后用勾股定理即可得出结论；
（3）①先求出EC=5，再求出D'C=1，根据勾股定理求出DH=，CH=，再判断出△EMN∽△EHD，得出，△ED'M∽△ECH，得出，进而得出，即可得出结论；
②先判断出∠MD'H=∠NED'，进而判断出∠MD'H=∠ECB，即可得出，即可．

(1)如图1，连接，在矩形中，，，

在中，根据勾股定理得，，

∵是中点，

∴，

∴，

∵，

∴，

∴，

∴∽，

∴，

∴，

∴设，

∴，

∴，

∴，

即：；

(2)如图2，在矩形中，

∵平分，

∴，

∵，

∴，

∴，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∵，

∴≌，

∴，

∴，

过点作于，

∴，

∴，，

∵，

∴∽，

∴，

设，

∴，

∴，

∴，

在中，；

(3)①在矩形中，，

∵，，

∴，

∵，

∴，

由折叠知，，，，

∴，

设，

∴，

根据勾股定理得，，

∴，

∴，，

∵，

∴，

∴，

∴∽，

∴，

∵，

∴，

∵，

∴∽，

∴，

∴，

∴，

∴；

②相似，理由：由折叠知，，，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴∽．