题目内容
 如图,E为正方形ABCD内一点,且∠BEC=90°,将△BEC绕B点旋转90°使BC与AB重合,得到△ABF,连EF交AB于P.已知BC=5,AF=4,则AP:BC的值为
如图,E为正方形ABCD内一点,且∠BEC=90°,将△BEC绕B点旋转90°使BC与AB重合,得到△ABF,连EF交AB于P.已知BC=5,AF=4,则AP:BC的值为
- A.3:5
- B.4:7
- C.3:4
- D.5:7
B
分析:可证明∠BCE=∠ABE,由∠BCE=∠BAF,得∠BAF=∠ABE,从而得出AF∥BE,△APF∽△BPE,则 =
= =
= ,即可得出AP:BC的值.
,即可得出AP:BC的值.
解答:根据题意得,△ABF∽△CBE,
∴∠BCE=∠BAF,
∵∠BCE+∠CBE=∠ABE+∠CBE=90°,
∴∠BCE=∠ABE,
∴∠BAF=∠ABE,
∴AF∥BE,
∴△APF∽△BPE,
∴ =
= ,
,
∵BC=5,AF=4,
∴CE=4,
∴BE=3,
∴ =
= =
= ,
,
∴AP:BC=4:7.
故选B.
点评:本题考查了相似三角形的判定和性质、勾股定理、正方形的性质以及旋转的性质,注意旋转前后两个三角形全等.
分析:可证明∠BCE=∠ABE,由∠BCE=∠BAF,得∠BAF=∠ABE,从而得出AF∥BE,△APF∽△BPE,则
 =
= =
= ,即可得出AP:BC的值.
,即可得出AP:BC的值.解答:根据题意得,△ABF∽△CBE,
∴∠BCE=∠BAF,
∵∠BCE+∠CBE=∠ABE+∠CBE=90°,
∴∠BCE=∠ABE,
∴∠BAF=∠ABE,
∴AF∥BE,
∴△APF∽△BPE,
∴
 =
= ,
,∵BC=5,AF=4,
∴CE=4,
∴BE=3,
∴
 =
= =
= ,
,∴AP:BC=4:7.
故选B.
点评:本题考查了相似三角形的判定和性质、勾股定理、正方形的性质以及旋转的性质,注意旋转前后两个三角形全等.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以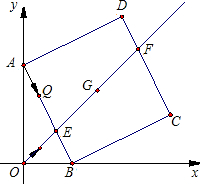 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.