��Ŀ����
����Ŀ����������������˾�����˽����2020���п���ʱǿ��Ҫע��ѧ���������������������Ҫ��ǿѧ���Ĵ��¾�����ۺ�����.����ʦ�볢�Ըı��ѧ�������������̻�ѧ�������Ϊ����ѧ����ѧϰ.�����������ε�ѧϰ�У�����ͬѧ�ǽ�������е�һ������ʱ�����������¹��̣���������ʦ��������⣩��
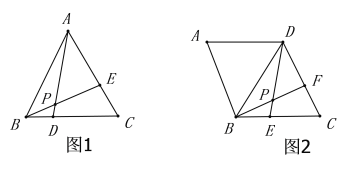
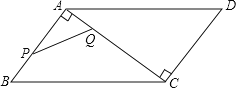
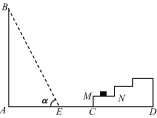
�ȳ�ʾ���⣨1��:��ͼ1���ڵȱ�������![]() �У�
�У�![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() Ϊ
Ϊ![]() ��һ�㣬���
��һ�㣬���![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() �Ķ���.
�Ķ���.
ͨ��ѧϰ������ʦ��ͬѧ��˵˵�Լ����ջ�.С��˵����һ�����ۣ�������ȱ�������![]() �У�ֻҪ����
�У�ֻҪ����![]() ����
����![]() �Ķ�������һ����ֵ�����ᷢ���ı�.����������ʦ��ʾ�����⣨2��:��ͼ2��������
�Ķ�������һ����ֵ�����ᷢ���ı�.����������ʦ��ʾ�����⣨2��:��ͼ2��������![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����
�����![]() ��
��![]() ��������εı߳�.
��������εı߳�.
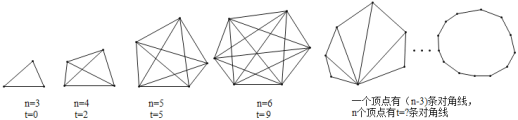
���⣨3����ͨ�����ϵ�ѧϰ��д����õ�����ʾ��һ�����ɣ�.
���𰸡���1��![]() ����2��
����2��![]() ����3���𰸲�Ψһ����������
����3���𰸲�Ψһ����������
��������
���⣨1������![]() �ǵȱ�������֤��
�ǵȱ�������֤��![]() ���ó�
���ó�![]() ���ٸ���������������ʼ��ɵ�֤��
���ٸ���������������ʼ��ɵ�֤��
���⣨2����![]() ��
��![]() �ڵ�
�ڵ�![]() �������ı���
�������ı���![]() �����εó�
�����εó�![]() ����
����![]() ���������Ǻ����������
���������Ǻ����������![]() ��
��![]() �������ݹ��ɶ����ó���.
�������ݹ��ɶ����ó���.
���⣨3���Ӹ��˵Ļ��ۺ��ĵ�дһ�仰����.
���⣨1����![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() .
.
��![]() ��
��
��![]() ��
��
��![]() .
.
��![]() ��
��
��![]() ��
��
���⣨2����ͼ����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��

���ı���![]() �����Σ�
������
��![]() ��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() .
.
�ɣ�1����֪![]() ��
��
��![]() ��
�У�
![]() ����
����![]() ��
��
��![]() ��
��
![]() ����
����![]() ��
��
��![]() .
.
��![]() ��
�У�
�ɹ��ɶ����ɵ�![]() ��
��
��![]() ��
��
��![]() ��
��
�����εı߳�Ϊ![]() .
.
���⣨3����ƽʱӦ��ע�����ͼ�εĻ��ۣ���ѧϰ���������������˵ȣ���֮��������.