题目内容
如图，有长为30m的篱笆，一面利用墙(墙的最大可用长度为10m)，围成中间隔有一道篱笆(平行于AB)的矩形花圃．设花圃的一边AB为xm，面积为ym2．
(1)求y与x的函数关系式；
(2)如果要围成面积为63m2的花圃，AB的长是多少？
(3)能围成比63m2更大的花圃吗？如果能，请求出最大面积；如果不能，请说明理由．
（1）y=x(30-3x),即y=-3x+30 (3分）
（2）当y=63时，-3x2+30x=63,解得：x1=3,x2=7
当x=3时，30-3x=21>10(不合题意舍去）
当x=7时，30-3x=9<10,符合题意
所以，当AB的长为7m时，花圃的面积为63(m2). （3分）
（3）能。y=-3x2+30x=-3(x-5) 2+75
由题意：0<30-3x≤10,得
≤x<10,
又当x>5时y随x的增大而减小
所以当x=时面积最大，最大面积为66
。 （3分）
练习册系列答案
相关题目
篱笆（平行于AB）的矩形花圃．设花圃的一边AB为xm，面积为ym2．
如图，有长为30m的篱笆，一面利用墙围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为xm，面积为ym2．
）的矩形花圃，设花圃一边
m，面积为
．
与
的花圃，
）的矩形花圃，设花圃一边
m，面积为
．
与
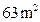的花圃，