Question

如图，在直角坐标系中，⊙A的半径为4，A的坐标为（2，0），⊙A与x轴交于E、F两点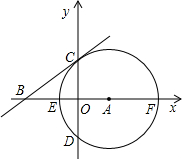，与y轴交于C、D两点，过C点作⊙A的切线BC交x轴于B．
（1）求直线BC的解析式；
（2）若一抛物线与x轴的交点恰为⊙A与x轴的两个交点，且抛物线的顶点在直线上y=

3

3

x+2上，求此抛物线的解析式；
（3）试判断点C是否在抛物线上，并说明理由．

Answer 1

分析：（1）连接AC，由Rt△AOC∽Rt△COB?

AO

OC

=

OC

OB

，求得OB的长，即可得出确定B点坐标，进而可根据B、C坐标用待定系数法求得BC直线的解析式．
（2）根据圆心的坐标及圆的半径不难得出E、F的坐标．根据抛物线和圆的对称性可知：抛物线顶点和圆心的横坐标必相等，据此可根据直线BC的解析式求出抛物线的顶点坐标．然后根据E、F及顶点坐标求出抛物线的解析式．
（3）在（1）中已经求得C点坐标，将C点坐标代入抛物线的解析式中进行判断即可

解答：解：（1）连接AC，则AC⊥BC．
∵OA=2，AC=4，
∴OC=2

3

．
又∵Rt△AOC∽Rt△COB，
∴

AO

OC

=

OC

OB

．
∴OB=6．
∴点C坐标为（0，2

3

），点B坐标为（-6，0）．
设直线BC的解析式为y=kx+b，
可求得直线BC的解析式为y=

3

3

x+2

3

．

（2）由题意得，⊙A与x轴的交点分别为E（-2，0）、F（6，0），
抛物线的对称轴过点A为直线x=2．
∵抛物线的顶点在直线y=

3

3

x+2上，
∴抛物线顶点坐标为（2，

2 3

3

+2）．
设抛物线解析式为y=a（x-2）²+（

2 3

3

+2）．
∵抛物线过点E（-2，0），
∴0=a（-2-2）²+

2 3

3

+2．
解得a=-

3

24

-

1

8

．
∴抛物线的解析式为y=（-

3

24

-

1

8

）（x-2）²+

2 3

3

+2．
即y=-

3+ 3

24

x2 +

3+ 3

6

x+

3+ 3

2

．

（3）∵点C的坐标是（0，2

3

）．
抛物线与y轴的交点坐标为（0，

3 +3

2

），
∴点C不在抛物线上．

点评：本题主要考查了二次函数的综合，在解题时要结合圆的相关知识、二次函数解析式的确定、相似三角形的判定和性质等知识点综合起来运用是本题的关键．