题目内容
如图10-1,在△A B B′和△A C C′中,∠B A B′=∠C A C′=m°,AC=AC',AB=AB'.
(1)不添加辅助线的前提下,请写出图中满足旋转变换的两个三角形分别是: ;旋转角度是 °;
(2)线段BC、B'C'的数量关系是: ;试求出BC、B'C'所在直线的夹角: ;

(3)随着△ACC'绕点A的旋转,(2)的结论是否依然成立?请从图10-2、图10-3中任选一个证明你的结论;
(4)利用解决上述问题所获得的经验探索下面的问题:如图10-4,等边△ABC外一点D,且∠BDC=60°,连接AD,试探索线段AD、CD、BD的数量关系.
(1)△A B C和△A B′ C′;旋转角度是m°
(2)线段BC=B'C', BC、B'C'所在直线的夹角:m°或(180- m )°
(3)成立,证明略。
(4)BD=" MD" + BM =AD+DC,证明略。
解析
(1)
△A B C和△A B′ C′;旋转角度是m°; ……………………2分
(2)
线段BC=B'C', BC、B'C'所在直线的夹角:m°或(180- m )°;………………3分

 (3)成立
(3)成立
图10-2、在△A B C和△A B′ C′中,
∠B A B′=∠C A C′=m°,AC=AC',AB=AB'
∠B A C =∠B A B′+∠C′A B,
∠B′ A C′=∠C A C′+∠C′A B
即∠B A C=∠B′ A C′ ……………………4分 A B′ C′ ……………………5分
A B′ C′ ……………………5分
∴BC=B'C' ……………………6分
延长B'C'交BCG于点M,设AB与B′ C′交于点O
∵∠CBA =∠ C'B′A, ∠MOB =∠AOB′ ……………………7分 ∴∠BM C′=∠BA B′="m° " ……………………8分
∴∠BM C′=∠BA B′="m° " ……………………8分
(4)方法一:
BD=AD+DC
如图10-4,在BD上截取BM=CD,连结AM ……………………9分
∵等边△ABC,
∴∠BAC=∠BDC=60°
又∠BOA=∠DOC,
∴∠ ABM=∠ACD
∵AB=AC
∴ ……………………11分
……………………11分
∴BM=DC,AM=AD,∠BAM=∠CAD
∴∠BAC=∠MAD=60°
∴△AMD为等边三角形
∴MD=AD
∴BD=" MD" + BM ="AD+DC " ……………………12分
方法二:如图10-5,在BD上截取DM=DC,先证明△CMD为等边三角形,再证明△ADC≌△BMC;
方法三:如图10-6,延长DC至M,使得DM=DB,先证明△BMD为等边三角形,再证明△BDC≌△BMC;
仿照方法一给分.

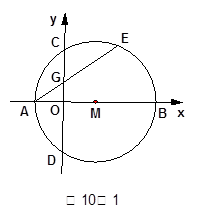




 中,点
中,点 在
在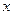 轴的正半轴上, ⊙
轴的正半轴上, ⊙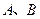 两点,交
两点,交 轴于
轴于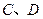 两点,且
两点,且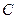 为
为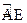 的中点,
的中点,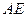 交
交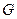 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),

 ,求证:
,求证: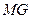 ∥
∥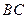
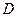 作⊙
作⊙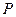 .动点
.动点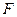 在⊙
在⊙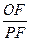 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律