Question

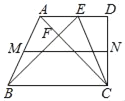
【题目】如图，在ABCD中，AD∥BC，AC＝BC＝4，∠D＝90°，M，N分别是AB、DC的中点，过B作BE⊥AC交射线AD于点E，BE与AC交于点F．

(1)当∠ACB＝30°时，求MN的长：

(2)设线段CD＝x，四边形ABCD的面积为y，求y与x的函数关系式及其定义域；

(3)联结CE，当CE＝AB时，求四边形ABCE的面积．

Answer 1

【答案】(1)MN＝2+；(2)y＝x2x(0＜x＜4)；(3)8或8．

【解析】

（1）解直角三角形求出AD，利用梯形中位线定理即可解决问题；
（2）求出AD，利用梯形的面积公式计算即可；
（3）作AG⊥BC于G，EH⊥BC于H．想办法证明△ABC≌△ECB，推出AC=BE=4，因为AC⊥BE，可得S四边形ABCE=ACBE，由此计算即可；

(1)∵AD∥BC，

∴∠DAC＝∠ACB＝30°，

在Rt△ACD中，∵AC＝4，∠D＝90°，∠ACD＝30°，

∴CD＝AC＝2，AD＝CD＝2，

∵AM＝BM，DN＝CN，

∴MN是梯形ABCD的中位线，

∴MN＝(AD+BC)＝2+．

(2)在Rt△ACD中，∵AC＝4，∠D＝90°，CD＝x，

∴AD＝＝，

∴y＝(AD+BC)CD＝(+4)x＝x+2x(0＜x＜4)．

(3)①当点E在线段AD上时，作AG⊥BC于G，EH⊥BC于H．

∵AD∥BC，AG⊥BC于G，EH⊥BC于H．

∴AG＝EH，∠AGB＝∠EHC＝90°，

∵AB＝EC，

∴Rt△ABG≌Rt△ECH，

∴∠ABC＝∠ECB，

∵AB＝EC，BC＝CB，

∴△ABC≌△ECB，

∴AC＝BE＝4，

∵AC⊥BE，

∴S四边形ABCE＝ACBE＝×4×4＝8．

②当点E在AD的延长线上时，易证四边形ABCE是平行四边形，

∵BE⊥AC，

∴四边形ABCE是菱形，

∵BC＝AC＝AB，

∴△ABC，△ACE是等边三角形，

∴S四边形ABCE＝2××42＝8．