题目内容
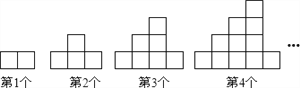
【题目】如图，下列图案均是由长度相同的火柴按一定的规律拼搭而成，围成的每个小正方形面积为1
.第一个图案面积为2，第二个图案面积为4，第三个图案面积为7，…依此规律，第8个图案面积为（ ）
A. 34 B. 35 C. 36 D. 37
【答案】D
【解析】分析：求出前4个图形中的所有正方形的面积，从而得到图案中面积的规律，再根据规律写出第n个图案中的面积即可．
详解：第1个图案面积为1+1=2cm2，
第2个图案面积为1+2+1=4cm2，
第3个图案面积为1+2+3+1=7cm2，
第4个图案面积为1+2+3+4+1=11cm2，
…
∴第n个图案面积为1+2+3+4+…+n+1=
n（n+1）+1cm2．
∴第8个图案面积为1+2+3+4+5+6+7+8+1=37cm2．
故选D．
练习册系列答案
相关题目
【题目】某学校计划组织全校1500名师生外出参加集体活动．经过研究，决定租用当地租车公司一共60辆
、
两种型号客车作为交通工具．
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注：载客量指的是每辆客车最多可载该校师生的人数．
学校租用型号客车
辆，租车总费用为
元．
(1)求与的函数解析式，请直接写出的取值范围；
(2)若要使租车总费用不超过22000元，一共有几种租车方案？并结合函数性质说明哪种租车方案最省钱？
