题目内容
如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F。


(1)如图2,当BP=BA时,∠EBF=____°,猜想∠QFC=____°;
(2)如图1,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明;
(3)已知线段AB= ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式。
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式。
(2)如图1,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明;
(3)已知线段AB=
 ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式。
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式。| 解:(1)∠EBF=30°,∠QFC=60°; (2)∠QFC=60°, 不妨设BP>  ,如图1所示, ,如图1所示,∵∠BAP=∠BAE+∠EAP=60°+∠EAP, ∠EAQ=∠QAP+∠EAP=60°+∠EAP, ∴∠BAP=∠EAQ, 在△ABP和△AEQ中, AB=AE,∠BAP=∠EAQ,AP=AQ, ∴△ABP≌△AEQ(SAS), ∴∠AEQ=∠ABP=90°, ∴∠BEF=  , ,∴∠QFC=  30°+30°=60°; 30°+30°=60°;(3)在图1中,过点F作FG⊥BE于点G, ∵△ABE是等边三角形, ∴BE=AB=  , ,由(1)得  30°, 30°,在Rt△BGF中,  , ,∴BF=  , ,∴EF=2, ∵△ABP≌△AEQ, ∴QE=BP=x, ∴QF=QE+EF=x+2, 过点Q作QH⊥BC,垂足为H, 在Rt△QHF中,  (x>0) (x>0)即y关于x的函数关系式是:  。 。 |
  |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
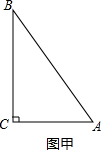 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.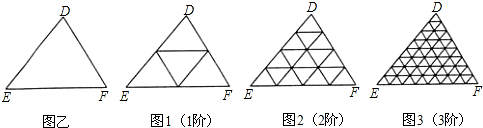
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

