题目内容
【题目】综合实践:
问题情境
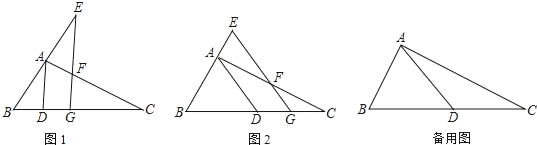
数学活动课上，老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图I，在正方形
中，点
为边
的中点.将
以点
为旋转中心，顺时针方向旋转，当点的对应点
落在边
上时，连接
.
“兴趣小组”发现的结论是:
；
“卓越小组”发现的结论是:
.
解决问题
(1)请你证明“兴趣小组”和“卓越小组”发现的结论；
拓展探究
证明完“兴趣小组”和“卓越小组”发现的结论后，“智慧小组”提出如下问题:如图2，连接
，若正方形的边长为
，求出的长度.
(2)请你帮助智慧小组写出线段的长度.(直接写出结论即可)
【答案】(1)①见解析；②见解析；(2) 
【解析】
(1)①根据旋转的性质，得到：
，进而得到：
，即可得到结论；
②先证：
，可得：
，利用余角的性质，进而可得：
，即可得到结论；
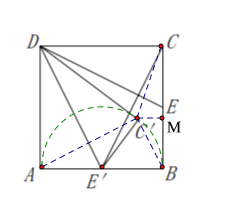
连接AC′，BC′，过C′作C′M⊥BC于点M，易证：点C′在以E′为圆心，E′A为半径的圆上，即：∠A C′B=90°，进而得到：tan∠BA C′=tan∠AD E′=
，由AB=2，
得：BC′=
，
=
，
，
，在RtCMC′中，利用勾股定理，即可求解.
(1)①
由
旋转得到，
.
又
四边形
是正方形，
.
，
(HL)，
；
②点
为
中点，
，AB=BC，
点
为
的中点.
，
又
(SAS)，
.
连接AC′，BC′，过C′作C′M⊥BC于点M，
∵E′A= E′B= E′C′，
∴点C′在以E′为圆心，E′A为半径的圆上，
∴∠A C′B=90°，
∵DA E′与D C′E′关于直线D E′轴对称，
∴AC′⊥D E′，
∴∠BA C′+∠A E′D=90°，
∵∠AD E′+∠A E′D=90°，
∴∠BA C′=∠AD E′，
∴tan∠BA C′=tan∠AD E′=，即：BC′： AC′：AB=1：2：
，
∵AB=2，
∴BC′=
，
∵∠A BC′+∠MB C′=90°，∠A BC′+∠BAC′=90°，
∴∠MB C′=∠BAC′，
∴MC′：MB：B C′=1：2：，
∴
=，
，
∴，
∴在RtCMC′中，CC′=
.
