题目内容
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
(1)图中∠AOF的余角是______(把符合条件的角都填出来).
(2)图中除直角相等外,还有相等的角,请写出三对:
①______;②______;③______.
(3)①如果∠AOD=140°.那么根据______,可得∠BOC=______度.
②如果 ,求∠EOF的度数.
,求∠EOF的度数.
解:(1)根据图形可得:∠AOC、∠EOF、∠BOD都是∠AOF的余角;
(2)∠AOC=∠EOF=∠BOD,∠COE=∠BOF,∠AOD=∠COB,∠AOF=∠DOE;
(3)①对顶角相等,∠BOC=∠AOD=140°.
②∠EOF=X°,则∠AOD=5x°,
由∠EOF+∠DOE=90°,∠DOE+∠BOD=90°,
∴∠BOD=∠EOF=x°,又∠AOD+∠BOD=180°,
所以x+5x=180,
解得x=30,∠EOF=30°
分析:(1)根据图形及余角的定义可得出答案.
(2)根据图形可找出三对相等角.
(3)观察图形可知∠AOD和∠BOC是对顶角,由此可得出答案.
点评:本题考查余角和补角的知识,有一定难度,关键是仔细地观察图形,注意不要遗漏满足条件的角.
(2)∠AOC=∠EOF=∠BOD,∠COE=∠BOF,∠AOD=∠COB,∠AOF=∠DOE;
(3)①对顶角相等,∠BOC=∠AOD=140°.
②∠EOF=X°,则∠AOD=5x°,
由∠EOF+∠DOE=90°,∠DOE+∠BOD=90°,
∴∠BOD=∠EOF=x°,又∠AOD+∠BOD=180°,
所以x+5x=180,
解得x=30,∠EOF=30°
分析:(1)根据图形及余角的定义可得出答案.
(2)根据图形可找出三对相等角.
(3)观察图形可知∠AOD和∠BOC是对顶角,由此可得出答案.
点评:本题考查余角和补角的知识,有一定难度,关键是仔细地观察图形,注意不要遗漏满足条件的角.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
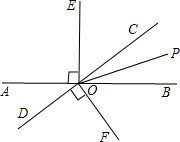 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.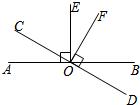 8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对:
8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对: 10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有
10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有 如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=
如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=