Question

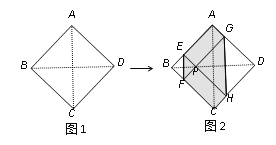
【题目】如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．

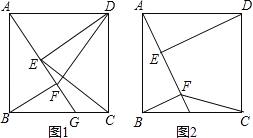
（1）求证：AE=BF；

（2）如图1，连接DF、CE，探究线段DF与CE的关系并证明；

（3）如图2，若AB=，G为CB中点，连接CF，直接写出四边形CDEF的面积．

Answer 1

【答案】(1)证明见解析；（2）DF=CE且DF⊥CE．理由见解析.(3)3.

【解析】

试题（1）根据垂直的定义和平行线的性质求出∠AED=∠BFA=90°，根据正方形的性质可得AB=AD，∠BAD=∠ADC=90°，再利用同角的余角相等求出∠BAF=∠ADE，然后利用“角角边”证明△AFB和△DEA全等，根据全等三角形对应边相等可得AE=BF；

（2）根据同角的余角相等求出∠FAD=∠EDC，根据全等三角形对应边相等可得AF=DE，根据正方形的性质可得AD=CD，然后利用“边角边”证明△FAD和△EDC全等，根据全等三角形对应边相等可得DF=CE，全等三角形对应角相等可得∠ADF=∠DCE，再求出∠DCF+∠CDF=90°，然后根据垂直的定义证明即可；

（3）根据线段中点的定义求出BG，再利用勾股定理列式求出AG，然后利用△ABG的面积列出方程求出BF，再利用勾股定理列式求出AF，从而得到AE=EF，再根据线段垂直平分线上的点到两端点的距离相等可得DF=AD，然后根据对角线互相垂直的四边形的面积等于对角线乘积的一半列式计算即可得解．

试题解析：（1）证明：∵DE⊥AG于点E，BF∥DE且交AG于点F，

∴BF⊥AG于点F，

∴∠AED=∠BFA=90°，

∵四边形ABCD是正方形，

∴AB=AD且∠BAD=∠ADC=90°，

∴∠BAF+∠EAD=90°，

∵∠EAD+∠ADE=90°，

∴∠BAF=∠ADE，

在△AFB和△DEA中，

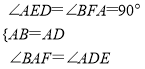
∴△AFB≌△DEA（AAS），

∴BF=AE；

（2）DF=CE且DF⊥CE．

理由如下：∵∠FAD+∠ADE=90°，∠EDC+∠ADE=∠ADC=90°，

∴∠FAD=∠EDC，

∵△AFB≌△DEA，

∴AF=DE，

又∵四边形ABCD是正方形，

∴AD=CD，

在△FAD和△EDC中，

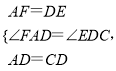
∴△FAD≌△EDC（SAS），

∴DF=CE且∠ADF=∠DCE，

∵∠ADF+∠CDF=∠ADC=90°，

∴∠DCF+∠CDF=90°，

∴△FAD≌△EDC（SAS），

∴DF=CE且∠ADF=∠DCE，

∵∠ADF+∠CDF=∠ADC=90°，

∴∠DCF+∠CDF=90°，

∴DF⊥CE；

（3）∵AB=，G为CB中点，

∴BG=BC=，

由勾股定理得，AG=

∵S△ABG=AG×BF=AB×BG

∴××BF=××

解得：BF=

由勾股定理得，AF=

∵△AFB≌△DEA，

∴AE=BF=

∴AE=EF=

∴DE垂直平分AF，

∴DF=AD=6，

由（2）知，DF=CE且DF⊥CE，

∴四边形CDEF的面积=DFCE=．