题目内容
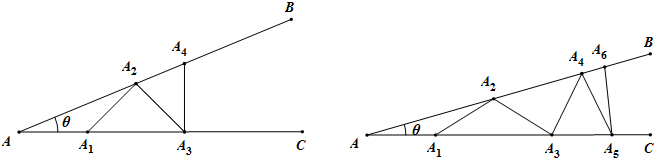
某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.
活动一:
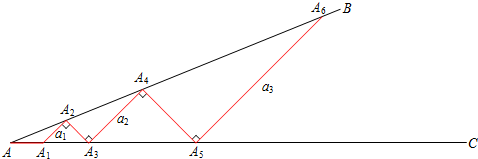
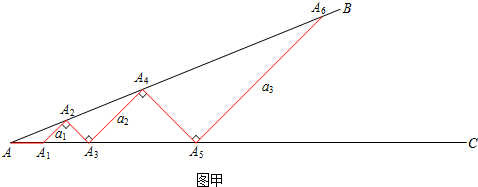
如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答:
(2)设AA1=A1A2=A2A3=1.
①θ=
②若记小棒A2n-1A2n的长度为an(n为正整数,如A1A2=a1,A3A4=a2,…) 求出此时a2,a3的值,并直接写出an(用含n的式子表示).
活动二:
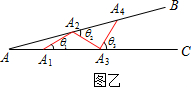
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,θ1=
(4)若只能摆放4根小棒,求θ的范围.
分析:(1)因为角的两条边为两条射线,没有长度,所以小棒可以无限摆放下去;
(2)①根据三角形外角的性质和等腰三角形的性质,即可推出,②结合已知条件,根据直角三角形的性质,即可得出A1A3=
,AA3=1+
,由A1A2∥A3A4∥A5A6,可以推出∠A=∠AA2A1=∠AA4A3=∠AA6A5,得AA3=A3A4,AA5=A5A6,即可推出a2、a3的长度,然后推出an的关于你的表达式;
(3)根据三角形外角的性质、等腰三角形的性质即可推出θ1=∠A2A1A3=2θ,即可推出θ2,同理即可推出θ2,θ3;
(4)根据(3)的结论,和三角形外角的性质,即可推出不等式,解不等式即可.
(2)①根据三角形外角的性质和等腰三角形的性质,即可推出,②结合已知条件,根据直角三角形的性质,即可得出A1A3=
| 2 |
| 2 |
(3)根据三角形外角的性质、等腰三角形的性质即可推出θ1=∠A2A1A3=2θ,即可推出θ2,同理即可推出θ2,θ3;
(4)根据(3)的结论,和三角形外角的性质,即可推出不等式,解不等式即可.
解答:解:(1)能.
因为角的两条边为两条射线,没有长度,所以小棒可以无限摆放下去;
(2)①∵AA1=A1A2=A2A3=1,A1A2⊥A2A3
∴θ2=45°,
θ=22.5°.
故答案为22.5;
②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3,
∴A1A3=
,AA3=1+
.
又∵A2A3⊥A3A4,
∴A1A2∥A3A4.
同理:A3A4∥A5A6,
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+
,
a3=AA3+A3A5=a2+A3A5.
∵A3A5=
a2,
∴a3=A5A6=AA5=a2+
a2=(
+1)2.
∴an=(
+1)n-1;
(3)∵A1A2=AA1
∴θ1=∠A2A1A3=2θ,
∴θ2=∠A2A4A3=θ+2θ=3θ,
∴θ3=∠A2A4A3+θ=4θ,
故答案为θ1=2θ,θ2=3θ,θ3=4θ;
(4)由题意得:
,
∴18°≤θ<22.5°.
因为角的两条边为两条射线,没有长度,所以小棒可以无限摆放下去;
(2)①∵AA1=A1A2=A2A3=1,A1A2⊥A2A3
∴θ2=45°,
θ=22.5°.
故答案为22.5;
②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3,
∴A1A3=
| 2 |
| 2 |
又∵A2A3⊥A3A4,
∴A1A2∥A3A4.
同理:A3A4∥A5A6,
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+
| 2 |
a3=AA3+A3A5=a2+A3A5.
∵A3A5=
| 2 |
∴a3=A5A6=AA5=a2+
| 2 |
| 2 |
∴an=(
| 2 |
(3)∵A1A2=AA1
∴θ1=∠A2A1A3=2θ,
∴θ2=∠A2A4A3=θ+2θ=3θ,
∴θ3=∠A2A4A3+θ=4θ,
故答案为θ1=2θ,θ2=3θ,θ3=4θ;
(4)由题意得:
|
∴18°≤θ<22.5°.
点评:本题主要考查相似三角形的判定和性质、勾股定理、解一元一次不等式、等腰直角三角形的性质等知识点,解题的关键在于找到等量关系,求相关角的度数等.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目