题目内容
【题目】如图,将两块完全相同的直角三角形纸片的直角顶点![]() 叠放在一起,若保持
叠放在一起,若保持![]() 不动,将
不动,将![]() 绕直角顶点
绕直角顶点![]() 旋转.
旋转.
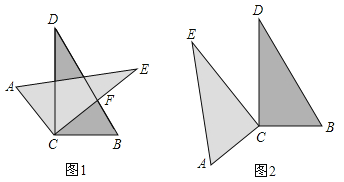
(1)当![]() 绕直角顶点
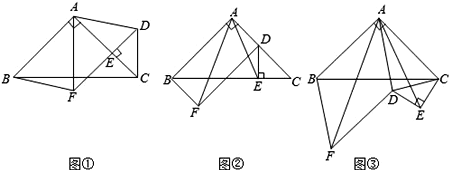
绕直角顶点![]() 旋转到如图1的位置时,
旋转到如图1的位置时,
①若![]() ,则
,则![]() =_________°;若
=_________°;若![]() ,则
,则![]() =_________°;
=_________°;
②猜想![]() 与
与![]() 的数量关系为:_________;
的数量关系为:_________;
(2)当![]() 绕直角顶点
绕直角顶点![]() 旋转到如图2的位置时,②中
旋转到如图2的位置时,②中![]() 与
与![]() 的数量关系是否仍然成立?请说明理由.(注:
的数量关系是否仍然成立?请说明理由.(注:![]() 与
与![]() 为小于平角的角)
为小于平角的角)
【答案】(1) ①144°;39°;②![]() +
+![]() =180°;(2)仍然成立,理由见详解
=180°;(2)仍然成立,理由见详解
【解析】
(1) ①由于是两直角三角形片的直角顶点![]() 叠放在一起,
叠放在一起,![]() ,可求出
,可求出![]() 的度数,再加∠ACE即可求出
的度数,再加∠ACE即可求出![]() 的度数;由
的度数;由![]() ,可求∠ECB得度数,即可求出
,可求∠ECB得度数,即可求出![]() 的度数;②由
的度数;②由![]() =90°+∠ECB ,
=90°+∠ECB ,![]() =90°-∠ECB ,相加即可得出结论;
=90°-∠ECB ,相加即可得出结论;
(2)将 ![]() 与
与![]() 相加即可得出结论.
相加即可得出结论.
解:(1) ①∵∠DCB=∠ACE=90°,![]() ,
,
∴∠ECB=90°36°=54°,
∴![]() =∠ACE+
=∠ACE+![]() =90°+54°=144°;
=90°+54°=144°;
若∵![]() ,
,
∴![]() =
=![]() -∠ACE=141°-90°=51°,
-∠ACE=141°-90°=51°,
∠DCE=90°51°=39°,
故答案为:144°;39°;
②![]() +
+![]() =180°.
=180°.
∵![]() =90°+∠ECB ,
=90°+∠ECB ,![]() =90°-∠ECB ,
=90°-∠ECB ,
∴![]() +
+![]() =90°+∠ECB+90°-∠ECB=180°,
=90°+∠ECB+90°-∠ECB=180°,
故答案为![]() +
+![]() =180°.
=180°.
(2) 仍然成立.
理由:∵∠ACE+∠DCE+∠DCB+∠ACB=360°,∠DCB=∠ACE=90°,
∴![]() +
+![]() =180°.
=180°.
故成立.

练习册系列答案
相关题目