Question

菱形的两邻角的度数之比为l：3，边长为5

2

，则高为

5

．

Answer 1

分析：菱形ABCD的边长BC=5

2

，CE为高，∠B：∠A=1：3，根据菱形的性质得AD∥BC，则∠A+∠B=180°，可计算出∠B=45°，而CE为高，得到△BCE为等腰直角三角形，根据等腰直角三角形的性质得CE=

2

2

BC，把BC=5

2

代入计算即可．

解答：解：如图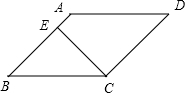，菱形ABCD的边长BC=5

2

，CE为高，∠B：∠A=1：3，
∵AD∥BC，
∴∠A+∠B=180°，
∴∠B+3∠B=180°，
∴∠B=45°，
而CE为高，
∴△BCE为等腰直角三角形，
∴BC=

2

CE，
∴CE=

2

2

BC=

2

2

×5

2

=5．
故答案为：5．

点评：本题考查了菱形的性质：菱形的对边分别平行，四条边都相等，两条对角线互相垂直平分，并且分别平分两组内角．也考查了等腰直角三角形的判定与性质．