Question

【题目】综合与实践：某“综合与实践”小组开展了“正方体纸盒的制作”实践活动，他们利用长为，宽为长方形纸板制作出两种不同方案的正方体盒子， 请你动手操作验证并完成任务．(纸板厚度及接缝处忽略不计)

动手操作一：

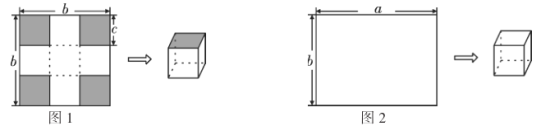
如图1，若，按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来就可以做成一个无盖的正方体纸盒．

问题解决：（1）此时，你发现与之间存在的数量关系为 ．

动手操作二：

如图2，若，现在在纸板的四角剪去两个小正方形和两个小长方形恰好可以制作成一个有盖的正方体纸盒，其大小与（1）中无盖正方体大小一样．

拓展延伸：（2）请你在图2中画出你剪去的两个小正方形和两个小长方形(用阴影表示)，折痕用虚线表示；

（3）此时，你发现与之间存在的数量关系为 ；若，求有盖正方体纸盒的表面积．

Answer 1

【答案】（1）；（2）见解析；（3）或或，600cm2

【解析】

（1）正方体是特殊的长方体，长宽高三者相等，故回到图形有.

（2）仔细思考，实际上是从大长方形纸中剪出一个正方形展开图，故从11种正方体展开图中选择合适的剪出形状即可.

（3）根据所剪的图形和正方体棱长都相等的性质，有，转化形式即可；将代入前面的等式求得和小正方体的棱长，根据正方体的表面积公式计算即可.

解：（1） (或)..

（2）所画图形如图所示(图形不唯一，画出一个即可).例如

（3） 据题意得，，

故或或

当时，.

由（1）可知制作的正方体的底面边长，

有盖正方体纸盒的表面积为.