题目内容
用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
若A(-
,y1)、B(
,y2)、C(
,y3)是该二次函数图象上的三点,则y1,y2,y3的大小关系是( )
| x | … | -1 | 0 | |||||||
| y | … | 2 | -1
|
-2 | -1
|
… |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| A、y2<y1<y3 |
| B、y1<y2<y3 |
| C、y3<y2<y1 |
| D、y2<y3<y1 |
分析:由表格可知,当x=0和x=2时函数值相等,则对称轴为直线x=1,a>0,则横坐标到x=1的距离越大,函数值越大.
解答:解:由表格可看出:对称轴为直线x=1,a>0,
由于|
-1|<|
-1|<|-
-1|,则y2<y3<y1,
故选D.
由于|
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
故选D.
点评:本题考查了二次函数图象上点的坐标特征,学会比较图象上点的坐标的大小.

练习册系列答案
相关题目

 的图象时,列了如下表格:
的图象时,列了如下表格:






 ,当
,当 时,函数值
时,函数值 。
。

 的图象时,列了如下表格:
的图象时,列了如下表格: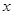


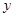



 ,当
,当 时,函数值
时,函数值 。
。