题目内容
 已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.
已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.
 解:顺时针旋转△BPC60度,可得△PBE为等边三角形.
解:顺时针旋转△BPC60度,可得△PBE为等边三角形.即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.
BM=BF•cos30°=BC•cos30°=
 ,
,则AM=1+
 =
=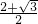 ,
,∵AB=BF,∠ABF=150°
∴∠BAF=15°
既得AF=
 =
=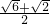 .
.分析:顺时针旋转△BPC60度,可得△PBE为等边三角形,若PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,求出AF的值即可.
点评:本题主要考查轴对称-路线最短问题的知识点,解答本题的关键是熟练掌握旋转的知识,此题难度一般.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 论是否仍然成立?请说明理由;
论是否仍然成立?请说明理由;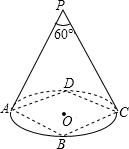 如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6m的正方形.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6m的正方形.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )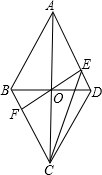 (2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F. 如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是
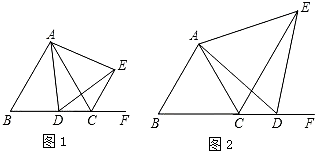
如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是 已知:E是边长为1的正方形ABCD对角线BD上一动点,点E从D点向B点运动(与点B、D不重合),过点E的直线MN平行于DC,交AD于点M,交BC于点N,EF⊥AE于点E,交CB(或CB的延长线)于点F.
已知:E是边长为1的正方形ABCD对角线BD上一动点,点E从D点向B点运动(与点B、D不重合),过点E的直线MN平行于DC,交AD于点M,交BC于点N,EF⊥AE于点E,交CB(或CB的延长线)于点F.