题目内容
【题目】如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．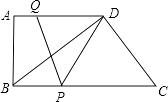 
（1）设△DPQ的面积为S，求S与t之间的函数关系式；
（2）当t为何值时，四边形PCDQ是平行四边形？
（3）分别求出当t为何值时，①PD=PQ，②DQ=PQ．
【答案】
（1）解：直角梯形ABCD中，AD∥BC，∠A=90°，BC=21，AB=12，AD=16，
依题意AQ=t，BP=2t，则DQ=16﹣t，PC=21﹣2t，
过点P作PE⊥AD于E，
则四边形ABPE是矩形，PE=AB=12，
∴S△DPQ= 
DQAB= （16﹣t）×12=﹣6t+96
（2）解：当四边形PCDQ是平行四边形时，PC=DQ，
∴21﹣2t=16﹣t解得：t=5，
∴当t=5时，四边形PCDQ是平行四边形
（3）解：∵AE=BP=2t，PE=AB=12，
①当PD=PQ时，QE=ED= QD，
∵DE=16﹣2t，
∴AE=BP=AQ+QE，即2t=t+16﹣2t，
解得：t= 
，
∴当t= 时，PD=PQ
②当DQ=PQ时，DQ2=PQ2
∴t2+122=（16﹣t）2解得：t= 
∴当t= 时，DQ=PQ
【解析】（1）S△QDP= DQAB，由题意知：AQ=t，DQ=AD﹣AQ=16﹣t，将DQ和AB的长代入，可求出S与t之间的函数关系式；（2）当四边形PCDQ为平行四边形时，PC=DQ，即16﹣t=21﹣2t，可将t求出；（3）当PD=PQ时，可得：AD=3t，从而可将t求出；当DQ=PQ时，根据DQ2=PQ2即：t2+122=（16﹣t）2可将t求出．
【考点精析】通过灵活运用勾股定理的概念和平行四边形的判定与性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积即可以解答此题．
阅读快车系列答案【题目】某欢乐谷为回馈广大谷迷，在暑假期间推出学生个人门票优惠价，各票价如下：
票价种类 | （A）学生夜场票 | （B）学生日通票 | （C）节假日通票 |
单价（元） | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生，其中购买的B种票数是A种票数的3倍还多7张，设购买A种票x张，C种票y张．
（1）直接写出x与y之间的函数关系式；
（2）设购票总费用为W元，求W（元）与x（张）之间的函数关系式；
（3）为方便学生游玩，计划购买的学生夜场票不低于20张，且每种票至少购买5张，则有几种购票方案？并指出哪种方案费用最少．
