题目内容

边长为8的正方形ABCD中，E、F是边AD、AB的中点，连接CE，取CE中点G，那么FG=
 
．
分析：根据题意，正方形ABCD的边长为8，E边AD的中点，可得出AE、BC的长；又由点F、G分别是AB、CE的中点，根据梯形的中位线定理，可得出FG的长；
解答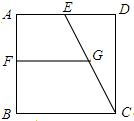：精英家教网解：如图，
∵正方形ABCD的边长为8，E、F是边AD、AB的中点，
∴AE=4，BC=8，
又∵点G是CE的中点，
∴FG为梯形ABCE的中位线，
∴EF=
1
2
(AE+BC)=
1
2
×（4+8）=6．
故答案为：6．
点评：本题主要考查了梯形的中位线定理，熟练掌握梯形的中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．
练习册系列答案
相关题目
已知点E是边长为2的正方形ABCD的AB边的延长线上一点，P为边AB上的一个动点（不与A、B重合），直线PF⊥PD，∠EBC的平分线与PF交于点Q．
（1）如图1，当P为AB的中点时，求PD的长，并比较PD与PQ长的大小；
（2）如图2，在点P运动过程中，PD与PQ长的大小关系会发生变化吗？为什么？
（3）设PB=x，△BPQ和△PAD的面积分别是S1、S2，又y=
S2S1
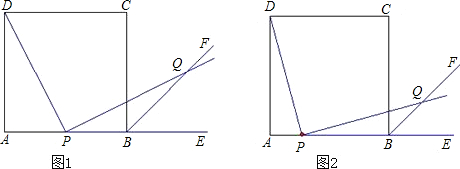
，试求y与x之间的函数关系式，并判断y随PB的变化而怎样变化？精英家教网
5、如图所示，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分的面积），验证了一个等式是（　　）
（2011•石家庄二模）阅读材料：
我们将能完全覆盖平面图形的最小圆称为该平面图形的最小覆盖圆．
例如：线段AB的最小覆盖圆就是以线段AB为直径的圆．
操作探究：
（1）如图1：已知线段AB与其外一点C，作过A、B、C三点的最小覆盖圆；（不写作法，保留作图痕迹）
（2）边长为1cm的正方形的最小覆盖圆的半径是
2
2
2
2
cm；
如图2，边长为1cm的两个正方形并列在一起，则其最小覆盖圆的半径是
5
2
5
2
cm；
如图3，半径为1cm的两个圆外切，则其最小覆盖圆的半径是
2
2
cm．
联想拓展：
⊙O1的半径为8，⊙O2，⊙O3的半径均为5．
（1）当⊙O1、⊙O2、⊙O3两两外切时（如图4），则其最小覆盖圆的半径是
40
3
40
3
；
（2）当⊙O1、⊙O2、⊙O3两两相切时，（1）中的结论还成立吗？如果不成立，则其最小覆盖圆的半径是
13
13
，并作出示意图．
如图，已知E是边长为12的正方形的边AB上一点，且AE=5，P是对角线AC上任意一点，则PE+PB的最小值是
13
13
．
如图，两个长方形的一部分重叠在一起，重叠部分是边长为3的正方形，则阴影部分的面积是
ab+cd-18
ab+cd-18
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网