Question

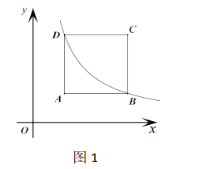
【题目】如图，二次函数y＝﹣x2+2（m﹣2）x+3的图象与x、y轴交于A、B、C三点，其中A（3，0），抛物线的顶点为D．

（1）求m的值及顶点D的坐标；

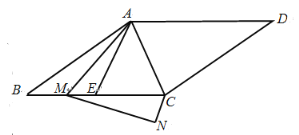
（2）如图1，若动点P在第一象限内的抛物线上，动点N在对称轴1上，当PA⊥NA，且PA＝NA时，求此时点P的坐标；

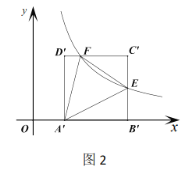
（3）如图2，若点Q是二次函数图象上对称轴右侧一点，设点Q到直线BC的距离为d，到抛物线的对称轴的距离为d1，当|d﹣d1|＝2时，请求出点Q的坐标．

Answer 1

【答案】（1）m＝3，(1，4)；（2）(1，2)；（3）(，2﹣7)

【解析】

（1）将点A的坐标代入函数表达式，即可求解；

（2）证明△NMA≌△AHP（AAS），则AH＝MN＝3﹣1＝2，即yP＝2＝﹣x2+2x+3，即可求解；

（3）已知点B，点C的坐标可求出直线BC的解析式，过点Q作y轴的平行线交BC于点M，则∠BCO=∠M，设点Q（t，﹣t2+2t+3），则点M（t，3t+3），则d＝DH＝MQ＝[（3t+3）﹣（﹣t2+2t+3）]，d1＝t﹣1，即可求解．

（1）将点A的坐标代入函数表达式得：0＝﹣32+2（m﹣2）×3+3，

解得：m＝3，

故抛物线的表达式为：y＝﹣x2+2x+3，

故点D的坐标为：（1，4）；

（2）过点A作y轴的平行线交过点N与x轴的平行线于点M，交过点P与x轴的平行线于点H，

∵∠NAM+∠PAH＝90°，∠NAM+∠ANM＝90°，

∴∠PAH＝∠ANM，

∵∠NMA＝∠AHP＝90°，AP＝NP，

∴△NMA≌△AHP（AAS），

∴AN＝MN＝3﹣1＝2，

即yP＝2＝﹣x2+2x+3，

解得：x＝（舍去负值），

故点P；

（3）设直线BC的表达式为：y＝kx+b，则，解得：，

由点B、C的表达式为：y＝3x+3，

如图2，过点Q作y轴的平行线交BC于点M，交x轴于点N，

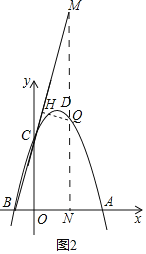
则MN∥y轴，

∴∠BCO＝∠M，而＝，则＝＝sin∠M，

过点Q作QH⊥BM，设点Q（t，﹣t2+2t+3），则点M（t，3t+3），

则d＝DH＝MQ＝ [（3t+3）﹣（﹣t2+2t+3）]，d1＝t﹣1，

∵|d﹣d1|＝2，即 [（3t+3）﹣（﹣t2+2t+3）]﹣（t﹣1）＝±2，

解得：t＝或﹣1（舍去），

故点Q的坐标为：．