题目内容
抛物线y=x2+(m-2)x-
m的图象与坐标轴有两个不同的交点,则m=
| 9 | 4 |
-1,-4,0
-1,-4,0
.分析:由于抛物线与x轴的交点不能确定,故应分两种情况进行讨论,即当抛物线经过原点时,此时抛物线与x轴还有一个除原点以外的交点;若抛物线不经过原点,则抛物线必与x轴有一个交点,此时△=0,求出两中情况是m的值即可.
解答:解:当抛物线经过原点时,y=-
m=0,解得m=0;
当抛物线不经过原点时,△=(m-2)2-3×1×(-
m)=0,解得m=-1或m=-4.
故答案为:-1,-4,0.
| 9 |
| 4 |
当抛物线不经过原点时,△=(m-2)2-3×1×(-
| 9 |
| 4 |
故答案为:-1,-4,0.
点评:本题考查的是抛物线与x轴的交点问题,解答此题时不要忽略抛物线过原点的情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点.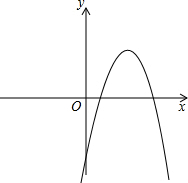 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4. 16、已知抛物线y=x2+bx+c的部分图象如图所示,若方程x2+bx+c=0有两个同号的实数根,则c的值可以是
16、已知抛物线y=x2+bx+c的部分图象如图所示,若方程x2+bx+c=0有两个同号的实数根,则c的值可以是