题目内容
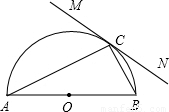
如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
(1)求∠ACM的度数.(2)在MN上是否存在一点D,使AB·CD=AC·BC,说明理由.

解:(1)连结BC,

![]() ∠B=62°.
∠B=62°.
MN是切线![]() ∠ACM=∠B=62°.
∠ACM=∠B=62°.
(2)过点B作BD⊥MN,则

![]() △ACB∽△CNB
△ACB∽△CNB
![]()
![]()
![]() AB·CD1=AC·BC.
AB·CD1=AC·BC.
过点A作AD2⊥MN,则

![]() △ABC∽△ACD2
△ABC∽△ACD2
![]()
![]()
![]() CD2·AB=AC·CB
CD2·AB=AC·CB

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
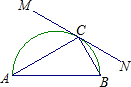 如图,已知直线MN与以AB为直径的半圆相切于点C,在MN上是否存在点D,使AB•CD=AC•BC( )
如图,已知直线MN与以AB为直径的半圆相切于点C,在MN上是否存在点D,使AB•CD=AC•BC( )| A、不存在 | B、存在一点 | C、存在二点 | D、存在无数点 |

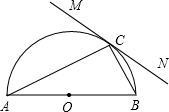 如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°. 如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.