题目内容
 如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与另一腰CD相切于点E,连接OD、OC、BE.
如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与另一腰CD相切于点E,连接OD、OC、BE.(1)求证:OD∥BE;
(2)若梯形ABCD的面积是48,设OD=x,OC=y,且x+y=14,求CD的长.
考点:切线的性质,全等三角形的判定与性质,勾股定理,梯形,圆周角定理
专题:几何综合题
分析:(1)连接OE,证出Rt△OAD≌Rt△OED,利用同弦对圆周角是圆心角的一半,得出∠AOD=∠ABE,利用同位角相等两直线平行得到OD∥BE,
(2)由Rt△COE≌Rt△COB,得到△COD是直角三角形,利用S梯形ABCD=2S△COD,
求出xy=48,结合x+y=14,求出CD.
(2)由Rt△COE≌Rt△COB,得到△COD是直角三角形,利用S梯形ABCD=2S△COD,
求出xy=48,结合x+y=14,求出CD.
解答:(1)证明:如图,连接OE,
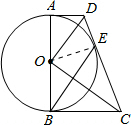
∵CD是⊙O的切线,
∴OE⊥CD,
在Rt△OAD和Rt△OED,
,
∴Rt△OAD≌Rt△OED(HL)
∴∠AOD=∠EOD=
∠AOE,
在⊙O中,∠ABE=
∠AOE,
∴∠AOD=∠ABE,
∴OD∥BE(同位角相等,两直线平行).
(2)解:与(1)同理可证:Rt△COE≌Rt△COB,
∴∠COE=∠COB=
∠BOE,
∵∠DOE+∠COE=90°,
∴△COD是直角三角形,
∵S△DEO=S△DAO,S△OCE=S△COB,
∴S梯形ABCD=2(S△DOE+S△COE)=2S△COD=OC•OD=48,
即xy=48,
又∵x+y=14,
∴x2+y2=(x+y)2-2xy=142-2×48=100,
在Rt△COD中,
CD=
=
=
=10,
∴CD=10.

∵CD是⊙O的切线,
∴OE⊥CD,
在Rt△OAD和Rt△OED,
,
|
∴Rt△OAD≌Rt△OED(HL)
∴∠AOD=∠EOD=
| 1 |
| 2 |
在⊙O中,∠ABE=
| 1 |
| 2 |
∴∠AOD=∠ABE,
∴OD∥BE(同位角相等,两直线平行).
(2)解:与(1)同理可证:Rt△COE≌Rt△COB,
∴∠COE=∠COB=
| 1 |
| 2 |
∵∠DOE+∠COE=90°,
∴△COD是直角三角形,
∵S△DEO=S△DAO,S△OCE=S△COB,
∴S梯形ABCD=2(S△DOE+S△COE)=2S△COD=OC•OD=48,
即xy=48,
又∵x+y=14,
∴x2+y2=(x+y)2-2xy=142-2×48=100,
在Rt△COD中,
CD=
| OC2+OD2 |
| x2+y2 |
| 100 |
∴CD=10.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、圆周角定理和全等三角形的判定与性质.关键是综合运用,找准线段及角的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: 如图,AE是⊙O的直径,DF切⊙O于B,AD⊥DF于D,EF⊥DF于F,AD交⊙O于C.
如图,AE是⊙O的直径,DF切⊙O于B,AD⊥DF于D,EF⊥DF于F,AD交⊙O于C.
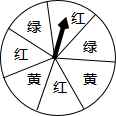 如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为
如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为