题目内容
已知:关于x的一元二次方程
(1)求m的值;
(2)当m取(1)中值时,求证:无论k取任何值原一元二次方程总没有实数根.
解:(1)根据题意得: ,
,
解①得:m=1或m=4,
解②得:m≠1且m≠2,
则m的值为:4;
(2)证明:∵当m=4时,方程为6x2+(3k+1)x+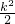 +1=0,
+1=0,
∴△=(3k+1)2-4×6×(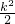 +1)=9k2+6k+1-12k2-24=-3k2+6k-23=-3(k-1)2-20,
+1)=9k2+6k+1-12k2-24=-3k2+6k-23=-3(k-1)2-20,
∵(k-1)2≥0,
∴-3(k-1)2≤0,
∴△=-3(k-1)2-20<0,
∴无论k取任何值原一元二次方程总没有实数根.
分析:(1)由一元二次方程的定义,可得 ,继而求得m的值;
,继而求得m的值;
(2)将m的值代入,可得方程6x2+(3k+1)x+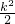 +1=0,即可得△=-3(k-1)2-20<0,即可判定无论k取任何值原一元二次方程总没有实数根.
+1=0,即可得△=-3(k-1)2-20<0,即可判定无论k取任何值原一元二次方程总没有实数根.
点评:此题考查了一元二次方程的解的定义与一元二次方程根的判别式的应用.此题难度适中,注意掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系,注意配方法的应用.
 ,
,解①得:m=1或m=4,
解②得:m≠1且m≠2,
则m的值为:4;
(2)证明:∵当m=4时,方程为6x2+(3k+1)x+
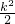 +1=0,
+1=0,∴△=(3k+1)2-4×6×(
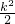 +1)=9k2+6k+1-12k2-24=-3k2+6k-23=-3(k-1)2-20,
+1)=9k2+6k+1-12k2-24=-3k2+6k-23=-3(k-1)2-20,∵(k-1)2≥0,
∴-3(k-1)2≤0,
∴△=-3(k-1)2-20<0,
∴无论k取任何值原一元二次方程总没有实数根.
分析:(1)由一元二次方程的定义,可得
 ,继而求得m的值;
,继而求得m的值;(2)将m的值代入,可得方程6x2+(3k+1)x+
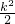 +1=0,即可得△=-3(k-1)2-20<0,即可判定无论k取任何值原一元二次方程总没有实数根.
+1=0,即可得△=-3(k-1)2-20<0,即可判定无论k取任何值原一元二次方程总没有实数根.点评:此题考查了一元二次方程的解的定义与一元二次方程根的判别式的应用.此题难度适中,注意掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系,注意配方法的应用.

练习册系列答案
相关题目