题目内容
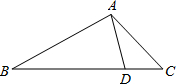 在△ABC中,AC=2,AB=3,BC=4,点D在BC边上,且CD=1
在△ABC中,AC=2,AB=3,BC=4,点D在BC边上,且CD=1
(1)求AD的长;
(2)点E是AB边上的动点(不与A、B重合)连接ED,作射线DF交AC边于点F,使∠EDF=∠BDA.请补全图形,说明线段BE与AF的比值是否为定值?请证明你的结论.
(1)解:在△ADC和△BAC中,
∵∠C=∠C,
 =
= =
= ,
,
∴△ADC∽△BAC,
∴ =
= ,
,
∵AB=3,
∴AD=1.5;
(2)如图所示:线段BE与AF的比值为定值2,
证明:∵∠EDF=∠BDA,
∴∠BDE=∠ADF,
∵△ADC∽△BAC,
∴∠B=∠DAF,
∴△BDE∽△ADF,
∴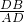 =
=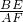 ,
,
∵BC=4,CD=1,AD=1.5,
∴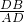 =
=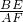 =
=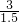 =2.
=2.
∴线段BE与AF的比值为定值2.
分析:(1)利用两边对应成比例且夹角相等得出△ADC∽△BAC,即可求出AD的长;
(2)利用已知得出∠BDE=∠ADF以及∠B=∠DAF,即可求出△BDE∽△ADF,进而利用对应边关系得出BE与AF的比值.
点评:此题主要考查了相似三角形的判定与性质,熟练应用相似三角形的判定与性质得出是解题关键.
∵∠C=∠C,
 =
= =
= ,
,∴△ADC∽△BAC,
∴
 =
= ,
,∵AB=3,
∴AD=1.5;
(2)如图所示:线段BE与AF的比值为定值2,
证明:∵∠EDF=∠BDA,
∴∠BDE=∠ADF,

∵△ADC∽△BAC,
∴∠B=∠DAF,
∴△BDE∽△ADF,
∴
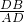 =
=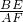 ,
,∵BC=4,CD=1,AD=1.5,
∴
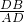 =
=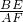 =
= =2.
=2.∴线段BE与AF的比值为定值2.
分析:(1)利用两边对应成比例且夹角相等得出△ADC∽△BAC,即可求出AD的长;
(2)利用已知得出∠BDE=∠ADF以及∠B=∠DAF,即可求出△BDE∽△ADF,进而利用对应边关系得出BE与AF的比值.
点评:此题主要考查了相似三角形的判定与性质,熟练应用相似三角形的判定与性质得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
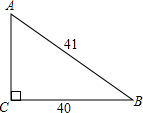 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=