题目内容
要使得关于x、y的多项式3x2-2kxy+4y2+| 1 | 2 |
分析:先将原多项式合并同类项,再令xy项的系数为0,然后解关于k的方程即可求出k.由于多项式中含xy的项有-2kxy+
xy,若不含xy项,则它们的系数为0,由此即可求出k的值.
| 1 |
| 2 |
解答:解:3x2-2kxy+4y2+
xy-x-2y+1=3x2+4y2-2kxy+
xy-x-2y+1.
因为不含xy项,
故-2k+
=0,
解得:k=
.
故填
.
| 1 |
| 2 |
| 1 |
| 2 |
因为不含xy项,
故-2k+
| 1 |
| 2 |
解得:k=
| 1 |
| 4 |
故填
| 1 |
| 4 |
点评:本题考查了合并同类项法则及对多项式“项”的概念的理解,题目设计巧妙,有利于培养学生灵活运用知识的能力.

练习册系列答案
相关题目
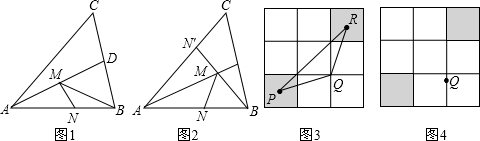
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?