题目内容
【题目】已知:直线![]() ,点
,点![]() 、
、![]() 分别在直线
分别在直线![]() ,
,![]() 上,点
上,点![]() 为平面内一点.
为平面内一点.
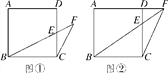
(![]() )如图,
)如图,![]() ,
,![]() ,
,![]() 的数量关系是__________.
的数量关系是__________.

(![]() )利用(
)利用(![]() )的结论解决问题:如图,已知
)的结论解决问题:如图,已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 得度数.
得度数.

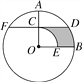
(![]() )如图,点
)如图,点![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.(用含
之间的数量关系.(用含![]() 的式子表示)
的式子表示)

【答案】(![]() )
)![]()
(![]() )
)![]()
(![]() )
)![]()
【解析】整体分析:
(1)过![]() 作
作![]() ,结合平行公理和平行线的性质即可得到
,结合平行公理和平行线的性质即可得到![]() ,
,![]() ,
,![]() 的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立
的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立![]() 之间的数量关系.
之间的数量关系.
解:(![]() )过
)过![]() 作
作![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
即:![]() .
.

(![]() )∵
)∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,由(
,由(![]() )结论可知,
)结论可知,
∴![]()
![]() ,
,
∴![]()
![]()
![]()
![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.

(![]() )
)![]() ,
,![]() ,
,![]() 之间的数量关系是
之间的数量关系是![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
得分(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 7 | 12 | 10 | 8 | 3 |
则得分的众数和中位数分别为( )
A.70分,70分
B.80分,80分
C.70分,80分
D.80分,70分