题目内容
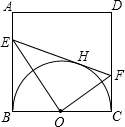
 已知:如图,正方形ABCD的边长是1,P是CD的中点,点Q是线段BC上一动点,当BQ为何值时,以A、D、P为顶点的三角形与以Q、C、P为顶点的三角形相似.
已知:如图,正方形ABCD的边长是1,P是CD的中点,点Q是线段BC上一动点,当BQ为何值时,以A、D、P为顶点的三角形与以Q、C、P为顶点的三角形相似.
分析:根据P是CD的中点以及正方形的四条边都相等的性质求出PD与PC的长度,再根据相似三角形对应边成比例的性质,分①当DP与PC是对应边,②当DP与CQ是对应边时,分别列出比例式求出CQ的长度,再根据正方形的边长是1即可求出BQ.
解答:解:∵正方形ABCD的边长是1,P是CD的中点,
∴PD=PC=
,
①当DP与PC是对应边时,
=
,
即
=
,
解得CQ=1,
∴BQ=BC-CQ=1-1=0;
②当DP与CQ是对应边时,
=
,
即
=
,
解得CQ=
,
∴BQ=BC-CQ=1-
=
,
综上所述,BQ的长度是0或
时,以A、D、P为顶点的三角形与以Q、C、P为顶点的三角形相似.
∴PD=PC=
| 1 |
| 2 |
①当DP与PC是对应边时,
| DP |
| PC |
| AD |
| CQ |
即
| ||
|
| 1 |
| CQ |
解得CQ=1,
∴BQ=BC-CQ=1-1=0;
②当DP与CQ是对应边时,
| DP |
| CQ |
| AD |
| PC |
即
| ||
| CQ |
| 1 | ||
|
解得CQ=
| 1 |
| 4 |
∴BQ=BC-CQ=1-
| 1 |
| 4 |
| 3 |
| 4 |
综上所述,BQ的长度是0或
| 3 |
| 4 |
点评:本题考查了正方形的四条边都相等的性质,相似三角形的对应边成比例的性质,因为对应边不明确,所以要分情况讨论求解,避免漏解而导致出错.

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.



 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.