题目内容
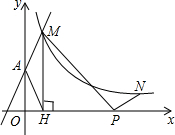 如图,直线y=2x+2与y轴交于A点,与反比例函数y=
如图,直线y=2x+2与y轴交于A点,与反比例函数y= (x>0)的图象交于点M,过M作MH⊥x轴于点 H,且tan∠AHO=2.点N(a,1)是反比例函数y=
(x>0)的图象交于点M,过M作MH⊥x轴于点 H,且tan∠AHO=2.点N(a,1)是反比例函数y= (x>0)图象上的点,若点P是在x轴上且使得PM+PN的长最小,则点P的坐标为________.
(x>0)图象上的点,若点P是在x轴上且使得PM+PN的长最小,则点P的坐标为________.
( ,0)
,0)
分析:先由y=2x+2确定A点坐标为(0,2),再利用正切的定义由tan∠AHO=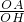 =2可计算出OH=1,则可确定M点坐标为(1,4),接着利用待定系数法得到反比例函数解析式为y=
=2可计算出OH=1,则可确定M点坐标为(1,4),接着利用待定系数法得到反比例函数解析式为y= ,于是把N(a,4)代入y=
,于是把N(a,4)代入y= 得a=1,则N点坐标为(4,1);作M点关于x轴的对称点M′,则M′的坐标为(1,-4),由于点P是在x轴上且使得PM+PN的长最小,则点P为直线NM′与x轴的交点,然后利用待定系数法确定直线NM′的解析式为y=
得a=1,则N点坐标为(4,1);作M点关于x轴的对称点M′,则M′的坐标为(1,-4),由于点P是在x轴上且使得PM+PN的长最小,则点P为直线NM′与x轴的交点,然后利用待定系数法确定直线NM′的解析式为y= x-
x- ,最后根据x轴上的坐标特点可确定P点坐标.
,最后根据x轴上的坐标特点可确定P点坐标.
解答: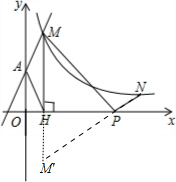 把x=0代入y=2x+2得y=2,则A点坐标为(0,2),
把x=0代入y=2x+2得y=2,则A点坐标为(0,2),
在Rt△AOH中,OA=2,tan∠AHO=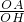 =2,
=2,
∴OH=1,
把x=1代入y=2x+2得y=4,
∴M点坐标为(1,4),
把M(1,4)代入y= 得k=1×4=4,
得k=1×4=4,
∴反比例函数解析式为y= ,
,
把N(a,4)代入y= 得4a=4,解得a=1,
得4a=4,解得a=1,
∴N点坐标为(4,1),
作M点关于x轴的对称点M′,如图,则M′的坐标为(1,-4),
∵点P是在x轴上且使得PM+PN的长最小,
∴点P为直线NM′与x轴的交点,
设直线NM′的解析式为y=mx+n,
把M′(1,-4)、N(4,1)代入得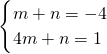 ,
,
解得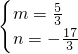 ,
,
∴直线NM′的解析式为y= x-
x- ,
,
把y=0代入得 x-
x- =0,解得x=
=0,解得x= ,
,
∴P点坐标为( ,0).
,0).
故答案为( ,0).
,0).
点评:本题考查了反比例函数的综合题,掌握反比例函数图象上点的坐标特征、待定系数法求函数解析式和锐角三角形函数的定义;熟练运用两点之间线段最短解决几何中关于距离最小的问题.
 ,0)
,0)分析:先由y=2x+2确定A点坐标为(0,2),再利用正切的定义由tan∠AHO=
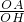 =2可计算出OH=1,则可确定M点坐标为(1,4),接着利用待定系数法得到反比例函数解析式为y=
=2可计算出OH=1,则可确定M点坐标为(1,4),接着利用待定系数法得到反比例函数解析式为y= ,于是把N(a,4)代入y=
,于是把N(a,4)代入y= 得a=1,则N点坐标为(4,1);作M点关于x轴的对称点M′,则M′的坐标为(1,-4),由于点P是在x轴上且使得PM+PN的长最小,则点P为直线NM′与x轴的交点,然后利用待定系数法确定直线NM′的解析式为y=
得a=1,则N点坐标为(4,1);作M点关于x轴的对称点M′,则M′的坐标为(1,-4),由于点P是在x轴上且使得PM+PN的长最小,则点P为直线NM′与x轴的交点,然后利用待定系数法确定直线NM′的解析式为y= x-
x- ,最后根据x轴上的坐标特点可确定P点坐标.
,最后根据x轴上的坐标特点可确定P点坐标.解答:
 把x=0代入y=2x+2得y=2,则A点坐标为(0,2),
把x=0代入y=2x+2得y=2,则A点坐标为(0,2),在Rt△AOH中,OA=2,tan∠AHO=
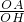 =2,
=2,∴OH=1,
把x=1代入y=2x+2得y=4,
∴M点坐标为(1,4),
把M(1,4)代入y=
 得k=1×4=4,
得k=1×4=4,∴反比例函数解析式为y=
 ,
,把N(a,4)代入y=
 得4a=4,解得a=1,
得4a=4,解得a=1,∴N点坐标为(4,1),
作M点关于x轴的对称点M′,如图,则M′的坐标为(1,-4),
∵点P是在x轴上且使得PM+PN的长最小,
∴点P为直线NM′与x轴的交点,
设直线NM′的解析式为y=mx+n,
把M′(1,-4)、N(4,1)代入得
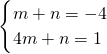 ,
,解得
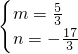 ,
,∴直线NM′的解析式为y=
 x-
x- ,
,把y=0代入得
 x-
x- =0,解得x=
=0,解得x= ,
,∴P点坐标为(
 ,0).
,0).故答案为(
 ,0).
,0).点评:本题考查了反比例函数的综合题,掌握反比例函数图象上点的坐标特征、待定系数法求函数解析式和锐角三角形函数的定义;熟练运用两点之间线段最短解决几何中关于距离最小的问题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.