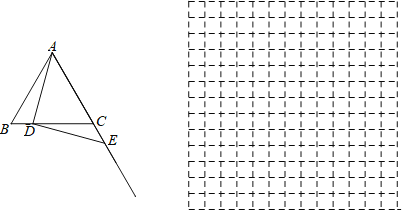题目内容
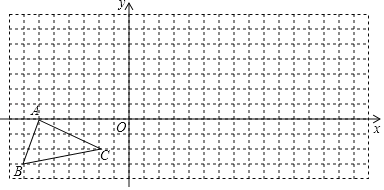
【题目】如图，△ABC在方格纸中，设单元正方形边长为1．
（1）已知△ABC的顶点都在格点上，请直接写出△ABC的面积S＝ ；
（2）请以点O为位似中心，相似比为2，在方格纸中将△ABC放大，画出放大后的图形△A′B'C'；
（3）求△A′B'C′的面积S′．
【答案】（1）7；（2）见解析；（3）28．
【解析】
（1）利用分割法求三角形面积即可．
（2）连接CO，延长CO到C′，使得OC′＝2OC，同法作出点A′，B′即可．
（3）利用相似三角形的性质解决问题即可．
（1）S△ABC＝3×5﹣
×1×3﹣×2×4﹣×1×5＝7；
故答案为7．
（2）△A′B′C′如图所示．
（3）△A′B′C′面积S′＝4S△ABC＝4×7＝28．
练习册系列答案
相关题目
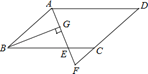
【题目】如图，在等边
中，
，点D是线段BC上的一动点，连接AD，过点D作
，垂足为D，交射线AC与点
设BD为xcm，CE为ycm．
小聪根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小聪的探究过程，请补充完整：
通过取点、画图、测量，得到了x与y的几组值，如下表：
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
|
|
|
| ___ |
| 0 |
|
|
|
| 0 |
说明：补全表格上相关数值保留一位小数
建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
结合画出的函数图象，解决问题：当线段BD是线段CE长的2倍时，BD的长度约为_____cm．
