题目内容
已知f（x）=
，求不等式（x+1）f（x+1）+x≤3的解集．
解：当x≥0时f（x+1）=1
则不等式变为（x+1）+x≤3，解得x≤1
当x＜0时f（x+1）=-1
则不等式变为-（x+1）+x≤3，解得x为任意实数
不等式（x+1）f（x+1）+x≤3的解集是x＜0．
分析：解不等式时，首先要把f（x+1）的形式化为一般形式，可以分x≥0和x＜0两种情况进行讨论．
点评：本题主要考查了一元一次不等式的求解，正确对x的范围讨论是解题的关键．
则不等式变为（x+1）+x≤3，解得x≤1
当x＜0时f（x+1）=-1
则不等式变为-（x+1）+x≤3，解得x为任意实数
不等式（x+1）f（x+1）+x≤3的解集是x＜0．
分析：解不等式时，首先要把f（x+1）的形式化为一般形式，可以分x≥0和x＜0两种情况进行讨论．
点评：本题主要考查了一元一次不等式的求解，正确对x的范围讨论是解题的关键．
练习册系列答案
相关题目
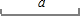
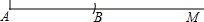
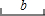
15、作图题（要求用直尺和圆规作图，写出作法，保留作图痕迹，不要求写出证明过程）
如图1，将等腰直角三角形纸片ABC沿底边上的高CD剪开，得到两个全等的三角形△ADC，△BDC，已知AC=4．