题目内容
解方程:
解:设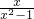 =y,
=y,
则原方程可化为
3y+ =5.
=5.
∴3y2-5y+2=0
解得,y=1,或y= .
.
当y=1时,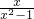 =1,
=1,
∴x2-x-1=0.
解得,x=
当y= 时,
时, ,
,
∴2x2-3x-2=0.
解得,x=- ,或x=2.
,或x=2.
经检验,它们都是原方程的根.
∴原方程的根是x1= ,x2=
,x2= ,x3=-
,x3=- ,x4=2.
,x4=2.
分析:由于 ,
, ,出现互为倒数的两个分式,设
,出现互为倒数的两个分式,设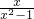 =y,将原方程转化为关于y的分式方程,先求y,再求x,结果要检验.
=y,将原方程转化为关于y的分式方程,先求y,再求x,结果要检验.
点评:本题中的两个式子互为倒数,可设其中的一个为y,那么另一个为它的倒数.
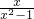 =y,
=y,则原方程可化为
3y+
 =5.
=5.∴3y2-5y+2=0
解得,y=1,或y=
 .
.当y=1时,
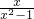 =1,
=1,∴x2-x-1=0.
解得,x=

当y=
 时,
时, ,
,∴2x2-3x-2=0.
解得,x=-
 ,或x=2.
,或x=2.经检验,它们都是原方程的根.
∴原方程的根是x1=
 ,x2=
,x2= ,x3=-
,x3=- ,x4=2.
,x4=2.分析:由于
 ,
, ,出现互为倒数的两个分式,设
,出现互为倒数的两个分式,设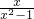 =y,将原方程转化为关于y的分式方程,先求y,再求x,结果要检验.
=y,将原方程转化为关于y的分式方程,先求y,再求x,结果要检验.点评:本题中的两个式子互为倒数,可设其中的一个为y,那么另一个为它的倒数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目