题目内容
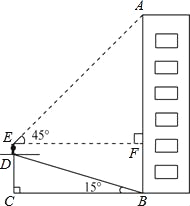
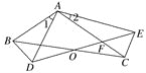
【题目】如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
【答案】(1)CF=![]() ;(2)tanD=
;(2)tanD=![]() .
.
【解析】
(1)证明△ABC∽△FAC,利用相似三角形的对应边成比例列式求解即可.
(2)过点C作CH⊥AB于点H,由余角的性质可知∠D=∠ECH,先由勾股定理求出AB的长,再根据面积法求出CH的长,再由勾股定理求出AH的长,继而可求出HE的长,然后根据正切的定义求解即可.
(1)∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC,
∴![]() ,即
,即![]() ,
,
解得CF=![]() ;
;
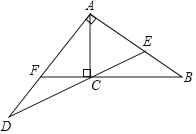
(2)如图,过点C作CH⊥AB于点H,

∵∠D+∠AED=90°, ∠ECH+∠AED=90°,
∴∠D=∠ECH.
∵AC=3,BC=4,
∴AB=5,
则CH=![]() ,
,
∴AH=![]() =
=![]() ,EH=AE﹣AH=
,EH=AE﹣AH=![]() ,
,
∴tanD=tan∠ECH=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.