题目内容
方程ax2+bx+c=0（a≠0）中，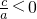
，那么该方程
- A.一定没有实数根
- B.一定有两个不相等的实数根
- C.一定又两个相等的实数根
- D.只有一个实数根
B
分析：根据根的判别式△=b2-4ac来判断该方程的根的情况．
解答：∵程ax2+bx+c=0（a≠0）中，，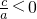
∴ac＜0，
∴-4ac＞0，
∴△=b2-4ac＞0，
∴该方程有两个不相等的实数根．
故选B．
点评：本题主要考查了一元二次方程的根的判别式．一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
分析：根据根的判别式△=b2-4ac来判断该方程的根的情况．
解答：∵程ax2+bx+c=0（a≠0）中，
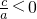，∴ac＜0，
∴-4ac＞0，
∴△=b2-4ac＞0，
∴该方程有两个不相等的实数根．
故选B．
点评：本题主要考查了一元二次方程的根的判别式．一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
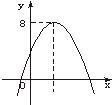9、已知抛物线y=ax2+bx+c如图所示，则关于x的方程ax2+bx+c-8=0的根的情况是（ ）
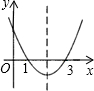己知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＜0；（2）方程ax2+bx+c=0两根都大于零；（3）y随x的增大而增大；（4）一次函数y=x+bc的图象一定不过第二象限．其中正确的个数是（ ）
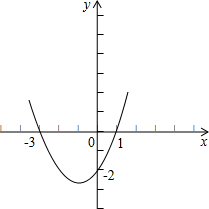已知函数y=ax2+bx+c的图象如图所示，试根据图象回答下列问题：