题目内容
【题目】二次函数 y＝ax2+bx+c（a≠0）的图象与 y 轴交于点（0，﹣2），且过点 A（﹣1，1）和 B（4，6）．
（1）求二次函数的解析式，并写出其图象的顶点坐标；
（2）当 2≤x≤5 时，求二次函数的函数值 y 的取值范围．
【答案】（1）该二次函数解析式为：y＝x2﹣2x﹣2，图象的顶点坐标为（1，﹣3）；（2）当 2≤x≤5 时，二次函数的函数值 y 的取值范围为﹣2≤y≤13．
【解析】
（1）利用待定系数法求解可得其解析式，将其配方成顶点式可得其顶点坐标；
（2）先由y＝（x﹣1）2﹣3知当x＞1时y随x的增大而增大，据此求出x＝2和x＝5时y的值即可得答案．
（1）根据题意，将（0，﹣2），（﹣1，1），（4，6）代入解析式，得：
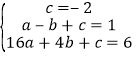，解得：
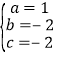，所以二次函数的解析式为y＝x2﹣2x﹣2＝（x﹣1）2﹣3，∴该二次函数的图象的顶点的坐标为（1，﹣3）．
（2）∵y＝（x﹣1）2﹣3，∴当x＞1时，y随x的增大而增大，当x＝2时，y＝﹣2；
当x＝5时，y＝13；
∴当2≤x≤5时，二次函数的函数值y的取值范围为﹣2≤y≤13．
练习册系列答案
相关题目
