Question

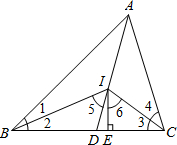如图，AD是△ABC的角平分线，∠1=∠2，∠3=∠4，IE⊥BC于点E，
（1）若∠ABC=40°，∠ACB=80°，则∠5=______，∠6=______．
（2）猜想∠5、∠6的数量关系是：______．
（3）请对你的猜想进行证明．

Answer 1

解：（1）∵∠ABC=40°，∠ACB=80°，
∴∠BAC=180°-40°-80°=60°，
∵AD是△ABC的角平分线，∠1=∠2，∠3=∠4，
∴∠5=∠1+∠BAD=20°+30°=50°，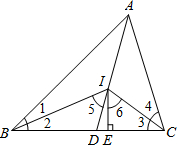
同理可得∠6=50°，
故答案为：50°，50°；

（2）猜想∠5=∠6；

（3）证明：∵∠5=∠BAD+∠1=（∠A+∠B）=（180°-∠C）=90°-∠C，
∠6=90°-∠3=90°-∠C，
∴∠5=∠6．
分析：（1）根据三角形的内角和定理可求出∠BAC的度数，利用角平分线和三角形的外角和定理即可求出∠5和∠6的度数；
（2）猜想∠5=∠6；利用三角形的外角和和直角三角形两锐角互余证明即可；
（3）利用三角形的外角和和直角三角形两锐角互余证明即可．
点评：本题考查了三角形的内角和定理、三角形的外角和定理和直角三角形两锐角互余的性质．