题目内容

AD是△ABC的角平分线，若∠BAC=60°，AD=8cm，AC=10cm，则△ACD的面积是________cm²．

20
分析：首先根据题意作图，然后过点D作DE⊥AC于E，由AD是△ABC的角平分线，∠BAC=60°，即可求得∠DAC的度数，又由AD=8cm，即可求得DE的长，继而可得△ACD的面积．
解答：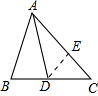

解：过点D作DE⊥AC于E，
∵AD是△ABC的角平分线，∠BAC=60°，
∴∠DAC= $\text{[math]}$ ∠BAC=30°，
在Rt△ADE中，DE= $\text{[math]}$ AD= $\text{[math]}$ ×8=4（cm），
∴S_△ACD= $\text{[math]}$ AC•DE= $\text{[math]}$ ×4×10=20（cm²）．
故答案为：20．
点评：此题考查了角平分线的性质与直角三角形的性质．此题难度不大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．