题目内容
规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k•b≠0,且|k|≠|b|)为互助一次函数,例如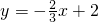 和
和 就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
(1)如图(1),当k=-1,b=3时,
①直接写出P点坐标:P______;
②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;
(2)如图(2),已知点M(-1,2),N(-2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.

 解:(1)①∵一次函数y=kx+b和它的互助一次函数的图象交于P点,
解:(1)①∵一次函数y=kx+b和它的互助一次函数的图象交于P点,k=-1,b=3时,
∴
 ,
,解得:
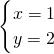 ,
,∴P(1,2);
故答案为:(1,2);
②如图(1),连接OQ,
∵y=-x+3与y=3x-1的图象l1,l2与x轴,y轴分别交于A,B点和C,D点.
∴A(3,0),B(0,3),C(
 ,0),D(0,-1).
,0),D(0,-1). ∵Q(m,3m-1),(
 ),
),∴S=S△OBQ+S△OCQ=
 =
= .
. ∴S△BCQ=S-S△BOC=
 =
= ,
,而S△ACP=
 =
= ,
,由S△BCQ=S△ACP,得
 =
= ,
,解得m=
 ;
; (2)由
 ,
,解得
 ,即P(1,k+b),
,即P(1,k+b),∴随着k,b值的变化,点P在直线x=1上运动,MP+NP的值随之发生变化.
如图(2),作点N(-2,0)关于直线x=1的对称点N′(4,0),
连接MN′交直线x=1于点P,则此时MP+NP取得最小值.
设直线MN′的解析式为y=cx+d,依题意
 ,
,解得
 ,
,∴直线MN′的解析式为
 .
. 令x=1,则
 ,
,∴P(1,
 ),
),即 使MP+NP取最小值时的P点坐标为(1,
 ).
).分析:(1)①当k=-1,b=3时得到两函数解析式,进而求出交点坐标即可;
②首先利用S=S△OBQ+S△OCQ=
 ,得出S△BCQ=S-S△BOC=
,得出S△BCQ=S-S△BOC= ,再利用S△ACP=
,再利用S△ACP= ,
,由S△BCQ=S△ACP,得
 =
= ,进而得出答案;
,进而得出答案;(2)作点N(-2,0)关于直线x=1的对称点N′(4,0),连接MN′交直线x=1于点P,则此时MP+NP取得最小值,进而得出直线MN′的解析式求出P点坐标即可.
点评:此题主要考查了一次函数综合以及利用轴对称求最短路径问题和待定系数法求一次函数解析式等知识,利用新定义理解互助一次函数定义是解题关键.

练习册系列答案
相关题目
我市某工艺厂为配合奥运会,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
| 销售单价x(元/件) | …… | 30 | 40 | 50 | 60 | …… |
| 每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
分析 (1)从表格中的数据我们可以看出当x增加10时,对应y的值减小100,所以y与x之间可能是一次函数的关系,我们可以根据图象发现这些点在一条直线上,所以y与x之间是一次函数的关系,然后设出一次函数关系式,求出其关系式.
(2)利用二次函数的知识求最大值.
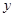 (元)与行李质量
(元)与行李质量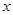 (千克)间的一次函数关系式为
(千克)间的一次函数关系式为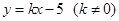 ,现知贝贝带了60千克的行李,交了行李费5元。
,现知贝贝带了60千克的行李,交了行李费5元。