题目内容
如图,△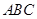 内接于⊙
内接于⊙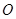 ,若⊙
,若⊙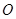 的半径为6,
的半径为6,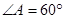 ,则
,则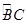 的长为____.
的长为____.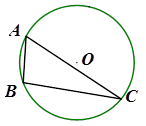
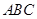 内接于⊙
内接于⊙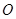 ,若⊙
,若⊙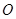 的半径为6,
的半径为6,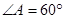 ,则
,则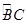 的长为____.
的长为____.

试题分析:连接OB、OC,根据圆周角定理可求得∠BOC的度数,再根据弧长公式求解即可.
连接OB、OC

∵
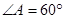
∴∠BOC=120°
∵⊙
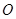 的半径为6
的半径为6∴
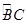 的长
的长 .
.点评:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.

练习册系列答案
相关题目
题目内容
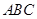 内接于⊙
内接于⊙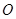 ,若⊙
,若⊙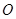 的半径为6,
的半径为6,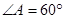 ,则
,则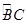 的长为____.
的长为____.


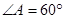
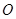 的半径为6
的半径为6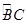 的长
的长 .
.