题目内容
已知,Rt△ABC在坐标系中,如图,∠A=90°,∠B=30°,C(-3,0),B(-9,0),
(1)将△ABC先向绕C顺时针旋转120°得到△A1B1C,则B1 的坐标为______;
(2)将△ABC沿x轴向右平移m个单位得到△A2 B2C1,当m=______时,A2在y轴上;
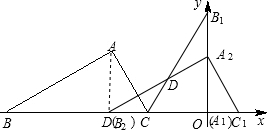
(3)画出△A1B1C和△A2 B2C1,并求出它们的重叠部分的面积.
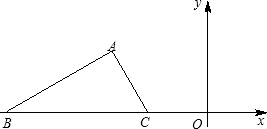
 解:(1)由题意得BC=6,∵∠A=90°,∠B=30°
解:(1)由题意得BC=6,∵∠A=90°,∠B=30°∴AC=3,
∴AB=3
 ,
,∵OB1=AB,
∴B1(0,3
 ),
),故答案为(0,3
 );
);(2)作AD⊥BC于点D,
∴BD=AB×cos30°=
 ,
,∴OD=
 ,
,故答案为
 ;
;(3)易得yB1C=
 x+3
x+3 ,yA2B2=
,yA2B2= x+
x+
∴点D的纵坐标为:

 ,
,S=
 ×
× ×
× -
- ×
× ×
×
 =
=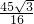 .
.分析:(1)易得BC的长,利用30°的三角函数值可得AC及BC长,旋转120°后,B1在y轴上,0B1=AB长;
(2)得到点A的横坐标,平移的距离为点A的横坐标的绝对值;
(3)易得B1C和A2B2的交点坐标,重叠部分的面积为S△A2B2O-S△B2CD,把相关数值代入即可.
点评:本题综合考查旋转变换及平移变换问题;得到旋转或平移后相关点的坐标是解决本题的突破点.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
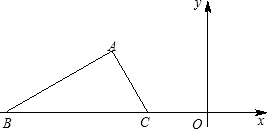
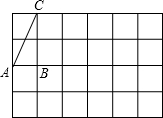
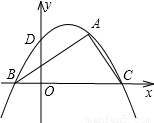
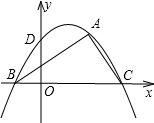 坐标为(2,
坐标为(2,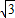 ),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
 ),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.