题目内容
【题目】如图，边长为2的正方形ABCD内接于⊙O，点E是 
上一点（不与A、B重合），点F是 
上一点，连接OE，OF，分别与AB，BC交于点G，H，有下列结论：
① 
= 
；
②△OGH是等腰三角形；
③四边形OGBH的面积随着点E位置的变化而变化；
④若BG=1﹣ 
，则BG，GE， 
围成的面积是 
+ 
．
其中正确的是（把所有正确结论的序号都填上）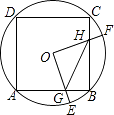
【答案】①②
【解析】如图所示，连接OC、OB、CF、BE．
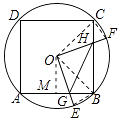
∵∠BOE+∠BOF=90°，∠COF+∠BOF=90°，
∴∠BOE=∠COF，
∴ 
= 
，
∵ 
= 
，
∴ 
= 
；故①正确，
在△BOG与△COH中，
，
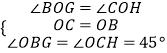∴△BOG≌△COH（ASA），
∴OG=OH，
∵∠HOG=90°
∴△OGH是等腰直角三角形，②正确，
∴S△OBG=S△OCH，
∴S四边形OGBH=S△BOC= 
S正方形ABCD=定值，故③错误；
作OM⊥AB于M，则OM=BM= 
AB=1，OB= 
OM= ，
∴GM= 
，
∴tan∠GOM= 
= ，
∴∠GOM=30°，
∵∠BOM=45°，
∴∠BOG=45°﹣30°=15°，
∴扇形BOE的面积= 
= 
，
∵BG=1﹣ ，
∴AG=1+ ，
过G作GP⊥BO于P，
∴PG=PB= 
﹣ 
，
∴△OBG的面积= × ×（ ﹣ ）= ﹣ 
，
∴BG，GE， 围成的面积=扇形BOE的面积﹣△BOG的面积= ﹣ + ，故④错误．
所以答案是：①②．
【考点精析】根据题目的已知条件，利用正多边形和圆和扇形面积计算公式的相关知识可以得到问题的答案，需要掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
